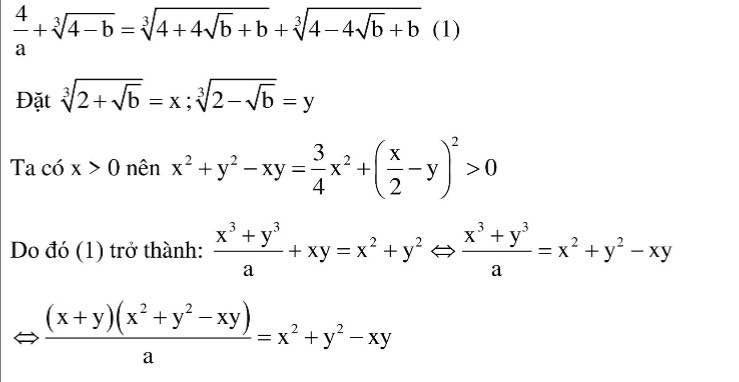đăng câu hỏi kiểu j mà đặng đc lên như thế này đấy
1.
Đặt \(\sqrt[3]{2+\sqrt{b}}=x;\sqrt[3]{2-\sqrt{b}}=y\)
Do \(x>0\Rightarrow x^2+y^2-xy=\dfrac{3}{4}x^2+\left(\dfrac{1}{2}x-y\right)^2>0\)
\(PT\Leftrightarrow\dfrac{x^3+y^3}{a}+xy=x^2+y^2\Leftrightarrow\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{a}=x^2-xy+y^2\\ \Leftrightarrow\left(x^2-xy+y^2\right)\left(\dfrac{x+y}{a}-1\right)=0\\ \Leftrightarrow\dfrac{x+y}{a}=1\\ \Leftrightarrow\sqrt[3]{2+\sqrt{b}}+\sqrt[3]{2-\sqrt{b}}=a\left(1\right)\\ \Leftrightarrow\left(\sqrt[3]{2+\sqrt{b}}+\sqrt[3]{2-\sqrt{b}}\right)^3=a^3\\ \Leftrightarrow4+3a\sqrt[3]{4-b}=a^3\left(2\right)\\ \Rightarrow4-b=\left(\dfrac{a^3-4}{3a}\right)^3\)
Mặt khác \(b\in \mathbb{Z^+}\)
\(\Rightarrow\left(a^3-4\right)⋮3a\Rightarrow\left(a^3-4\right)⋮a\\ \Rightarrow4⋮a\Rightarrow a\in\left\{1;2;4\right\}\)
Với \(a=1\Rightarrow4-b=1\Rightarrow b=5\)
Với \(a=2;a=4\Rightarrow b\notin \mathbb{Z}\)
Vậy \(\left(a;b\right)=\left(1;5\right)\)
\(x^3-y^3-6x^2+12x=27\)
\(\Leftrightarrow\left(x^3-6x^2+12x-8\right)-y^3=19\)
\(\Leftrightarrow\left(x-2\right)^3-y^3=19\)
\(\Leftrightarrow\left(x-y-2\right)\left[\left(x-2\right)^2+y\left(x-2\right)+y^2\right]=19\)
Phương trình ước số cơ bản (4 trường hợp), ví dụ: \(\left\{{}\begin{matrix}x-y-2=1\\\left(x-2\right)^2+y\left(x-2\right)+y^2=19\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y=x-3\\\left(x-2\right)^2+y\left(x-2\right)+y^2=19\end{matrix}\right.\)
Thế pt trên xuống dưới giải ra nghiệm nguyên