tính độ dài đường cao của hình chóp tứ giác đều với các kích thước như sau đáy là hình vuông cạnh 5 cm chiều dài cạnh bên là 10 cm

Những câu hỏi liên quan
Tính diện tích xung quanh của hình chóp tứ giác đều có độ dài cạnh bên là 13 cm và đáy là hình vuông cạnh 10 cm
Gọi M là trung điểm của AB:
\(\Rightarrow MA=MB=\dfrac{AB}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Do SM là ⊥ AB nên ΔSAM vuông tại M áp dụng định lý Py-ta-go ta có:
\(SA^2=SM^2+MA^2\)
\(\Rightarrow13^2=SM^2+5^2\)
\(\Rightarrow SM=\sqrt{13^2-5^2}=12\left(cm\right)\)
Nữa chu vi đáy của hình chóp tứ giác đều:
\(p=\dfrac{4\cdot10}{2}=20\left(cm\right)\)
Diện tích xung quanh của chóp tứ giác đều là:
\(S_{xq}=p\cdot d=20\cdot12=240\left(cm^2\right)\)
Ảnh tham khảo:
Đúng 3
Bình luận (0)
Gọi x (cm) là đường cao của mặt bên:
Ta có:
x² = 13² - 5² = 144
x = 12 (cm)
Diện tích xung quanh của hình chóp:
4 . 12 . 10 : 2 = 240 (cm²)
Đúng 1
Bình luận (0)
Cho hình chóp tứ giác đều S. ABCD có độ dài cạnh bên bằng 13 cm và đáy là hình vuông có cạnh bằng 10 cm. Tính diện tích xung quanh của hình chóp
Diện tích xung quanh hình chóp là:
$\dfrac12\cdot(4\cdot10)\cdot13=260(cm^2)$
Vậy diện tích xung quanh hình chóp là $260$ cm2.
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều \(A.MNPQ\) (Hình 5)
a) Hãy cho biết đỉnh, cạnh bên, mặt bên, cạnh đáy, mặt đáy, đường cao của hình chóp tứ giác đều đó.
b) Cho biết \(AM = 5\)cm, \(MN = 4\)cm. Tìm độ dài các cạnh \(AN\), \(AP\), \(AQ\), \(NP\), \(PQ\), \(QM\)

- Mặt bên: \(MAB\), \(MAC\), \(MBC\)
- Mặt đáy: \(ABC\)
- Đường cao: \(MO\)
- Độ dài cạnh bên: \(15\)cm
- Độ dài cạnh đáy: \(10\)cm
Đúng 0
Bình luận (0)
Câu hỏi 5. Túi quà có hình tứ giác đều
hình chóp (như hình) có cạnh đáy dài 10 cm và chiều cao cạnh
là 12cm.
a) Tính độ dài cạnh của túi quà
b) Tính diện tích xung quanh túi quà đó.
Cíu mình câu A vs
đề của thầy như thế á
ko có hình =(
như hình nhưng ko có hình
Đúng 0
Bình luận (0)
Tạo lập hình chóp tứ giác đều có độ dài cạnh đáy 4cm và cạnh bên 5cm theo hướng dẫn sau:- Trên một tấm bìa, vẽ một hình vuông và bốn hình tam giác cân với kích thước như Hình 9a.- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tứ giác đều như Hình 9b.
Đọc tiếp
Tạo lập hình chóp tứ giác đều có độ dài cạnh đáy 4cm và cạnh bên 5cm theo hướng dẫn sau:
- Trên một tấm bìa, vẽ một hình vuông và bốn hình tam giác cân với kích thước như Hình 9a.
- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tứ giác đều như Hình 9b.
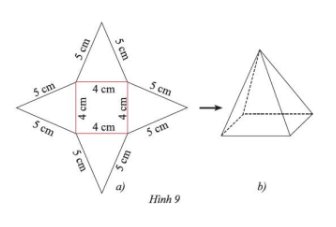
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như Hình 9b.
Đúng 0
Bình luận (0)
Một hôm, bạn An đánh rơi một mô hình kim tự tháp có dạng là hình chóp tứ giác đều vào một hộp đựng đầy nước dạng hình hộp chữ nhật. Biết hình hộp chữ nhật có kích thước đáy là 7x5 cm và chiều cao là 10 cm; còn hình chóp đều có chiều cao là 5 cm và cạnh đáy dài 6 cm. Hỏi khi vớt mô hình ra, lượng nước còn lại trong hộp là bao nhiêu?
Thể tích lượng nước còn lại trong hộp bằng hiệu giữa thể tích của hình hộp chữ nhật và thể tích của hình chóp đều. Vậy thể tích lượng còn lại là: 290 (cm3).
Đúng 0
Bình luận (0)
Một hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy là 10 cm, chiều cao hình chóp là 12 cm. Tính :
a) Diện tích toàn phần của hình chóp
b) Thể tích hình chóp
Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25 cm, đáy là hình vuông ABCD cạnh 30 cm
Tính diện tích toàn phần của hình chóp.
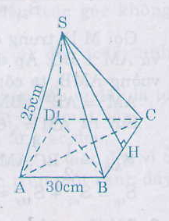
Ta có : \(d=SH=\sqrt{SB^2-BH^2}\)
\(=\sqrt{25^2-15^2}=\sqrt{400}=20\left(cm\right)\)
Diện tích xung quanh của hình chóp:
Sxq = pd = \(\dfrac{1}{2}\).30.4.20 = 1200 (cm2)
Diện tích đáy: Sđ = 302 = 900(cm2)
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sđ = 1200 + 900 = 2100(cm2)
Đúng 0
Bình luận (0)
Cho hình chóp đều S.ABCD có độ dài đường chéo của mặt đáy bằng 6 cm và cạnh bên bằng 5 cm.
a) Tính chiều cao hình chóp đều.
b) Tính diện tích tam giác SCD