Cho 2 đồ thị y=2x(d) và y=-3x+1(d'). Hãy chỉ ra phát biểu đúng
a) Điểm M(\(\dfrac{1}{5}\);\(\dfrac{2}{5}\)) thuộc cả d và d'
b) điểm P(-2;4) thuộc d mà không thuộc d'
c) Điểm Q(1;-2) chỉ thuộc d'
d) Điểm K(1;2) thuộc d' mà không thuộc d
Vẽ đồ thị các hàm số sau trên cùng 1 mặt phẳng tọa độ và tìm tọa độ giao điểm của 2 đường thẳng đó:
a) y = 2x và y = -3x + 5
b) y = 3x + 2 và y = \(-\dfrac{1}{2}x+1\)
c) y = \(\dfrac{3}{2}x-2\) và y = \(-\dfrac{1}{2}x\:+2\)
d) y = -2x + 5 và y = x + 2
Bạn tự vẽ nhé.
\(a,\) 2 đồ thị hàm số \(y=2x,y=-3x+5\) giao nhau khi và chỉ khi :
\(2x=-3x+5\\ \Leftrightarrow5x=5\\ \Leftrightarrow x=1\)
Thay \(x=1\) vào \(y=2x\Leftrightarrow y=2\)
Vậy giao điểm của 2 đồ thị là \(\left(1;2\right)\)
\(b,\) 2 đồ thị hàm số \(y=3x+2,y=-\dfrac{1}{2}x+1\) giao nhau khi và chỉ khi :
\(3x+2=-\dfrac{1}{2}x+1\\ \Leftrightarrow\dfrac{7}{2}x=-1\\ \Leftrightarrow x=-\dfrac{2}{7}\)
Thay \(x=-\dfrac{2}{7}\) vào \(y=3x+2\Rightarrow y=\dfrac{8}{7}\)
Vậy giao điểm của 2 đồ thị là \(\left(-\dfrac{2}{7};\dfrac{8}{7}\right)\)
\(c,\) 2 đồ thị hàm số \(y=\dfrac{3}{2}x-2,y=-\dfrac{1}{2}x+2\) giao nhau khi và chỉ khi :
\(\dfrac{3}{2}x-2=-\dfrac{1}{2}x+2\\ \Leftrightarrow2x=4\\ \Leftrightarrow x=2\)
Thay \(x=2\) vào \(y=\dfrac{3}{2}x-2\Rightarrow y=1\)
Vậy giao điểm của 2 đồ thị là \(\left(2;1\right)\)
\(d,\) 2 đồ thị hàm số \(y=-2x+5,y=x+2\) giao nhau khi và chỉ khi :
\(-2x+5=x+2\\ \Leftrightarrow-3x=-3\\ \Leftrightarrow x=1\)
Thay \(x=1\) vào \(y=x+2\Rightarrow y=3\)
Vậy giao điểm của 2 đồ thị là \(\left(1;3\right)\)
Bài 1: Cho hàm số \(y=x^3+3x^2+mx+m-2\) (m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành
Bài 2: Cho hàm số \(y=\dfrac{2x-2}{x+1}\) . Tìm m để đường thẳng d: \(y=2x+m\) cắt đồ thị (C) tại 2 điểm phân biệt A, B sao cho AB=\(\sqrt{5}\)
Bài 3: Cho hàm số \(y=\dfrac{1}{3}x^3-mx^2+2(m-1)x-3\) (m là tham số) có đồ thị là (Cm) . Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về cùng một phía đối với trục tung
Bài 4: Cho hàm số \(y=-x^3+2(m-1)x^2-(m^2-3m+2)x-4\)
(m là tham số) có đồ thị là (Cm). Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía của trục tung
Bài 5: Cho hàm số \(y=-x^3+3x^2+3(m^2-1)x-3m^2-1\) (1). Tìm m để hàm số (1) có cực đại, cực tiểu, đồng thời các điểm cực đại và cực tiểu cùng với gốc tọa độ O tạo thành một tam giác vuông tại O
1.
Đồ thị hàm bậc 3 có 2 điểm cực trị nằm về 2 phía trục hoành khi và chỉ khi \(f\left(x\right)=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow x^3+3x^2+mx+m-2=0\) có 3 nghiệm pb
\(\Leftrightarrow x^3+3x^2-2+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x-2\right)+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+m-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+m-2=0\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}1-2+m-2\ne0\\\Delta'=1-\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow m< 3\)
2.
Pt hoành độ giao điểm:
\(\dfrac{2x-2}{x+1}=2x+m\)
\(\Rightarrow2x-2=\left(2x+m\right)\left(x+1\right)\)
\(\Leftrightarrow2x^2+mx+m+2=0\) (1)
d cắt (C) tại 2 điểm pb \(\Rightarrow\) (1) có 2 nghiệm pb
\(\Rightarrow\Delta=m^2-8\left(m+2\right)>0\Rightarrow\left[{}\begin{matrix}m>4+4\sqrt{2}\\m< 4-4\sqrt{2}\end{matrix}\right.\)
Khi đó, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-\dfrac{m}{2}\\x_Ax_B=\dfrac{m+2}{2}\end{matrix}\right.\)
\(y_A=2x_A+m\) ; \(y_B=2x_B+m\)
\(\Rightarrow AB^2=\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2+\left(2x_A-2x_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2=1\)
\(\Leftrightarrow\left(x_A+x_B\right)^2-4x_Ax_B=1\)
\(\Leftrightarrow\left(-\dfrac{m}{2}\right)^2-4\left(\dfrac{m+2}{2}\right)=1\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10\\m=-2\end{matrix}\right.\)
3.
\(y'=x^2-2mx+2\left(m-1\right)\)
Hàm có 2 điểm cực trị nằm về cùng phía đối với trục tung khi và chỉ khi \(y'=0\) có 2 nghiệm pb cùng dấu
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-2\left(m-1\right)>0\\ac=1.2\left(m-1\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-2m+2>0\left(\text{luôn đúng}\right)\\m>1\end{matrix}\right.\)
\(\Leftrightarrow m>1\)
cho hai hàm số bậc nhất y = -2x + 5 (d) và y = \(\dfrac{1}{2}x\) (d')
a) Vẽ đồ thị của (d) và (d') của hai hàm số đã cho trên cùng một hệ tọa độ Oxy
b) Tìm tọa độ điểm M là giao điểm của 2 đồ thị vừa vẽ
b) Phương trình hoành độ giao điểm của (d) và (d') là:
\(-2x+5=\dfrac{1}{2}x\)
\(\Leftrightarrow-2x-\dfrac{1}{2}x=-5\)
\(\Leftrightarrow x\cdot\dfrac{-5}{2}=-5\)
hay \(x=-5:\dfrac{-5}{2}=-5\cdot\dfrac{2}{-5}=2\)
Thay x=2 vào (d), ta được:
\(y=-2\cdot2+5=-4+5=1\)
cho đường thẳng y=mx+n(Δ).Tìm m và n để đường thẳng (Δ) // với đường thẳng y=-2x+5(d) và có duy nhất 1 điểm chung với đồ thị (P)y=\(\dfrac{-1}{2}\)x2
Vì (Δ) // (d) \(\Rightarrow\left\{{}\begin{matrix}m=-2\\n\ne5\end{matrix}\right.\) \(\Rightarrow\left(\Delta\right):y=-2x+n\)
Phương trình hoành độ giao điểm của (Δ) và (P)
\(-2x+n=-\dfrac{1}{2}x^2\) \(\Leftrightarrow\dfrac{1}{2}x^2-2x+n=0\) (*)
Ta có: \(\Delta'=1-\dfrac{1}{2}n\)
Để (Δ) và (P) có 1 điểm chung duy nhất
\(\Leftrightarrow\) Phương trình (*) có nghiệm kép \(\Leftrightarrow1-\dfrac{1}{2}n=0\) \(\Leftrightarrow n=2\) (Thỏa mãn)
Vậy \(m=-2\) và \(n=2\)
Cho các phát biểu sau (1): Hàm số y = x 3 + 3 x 2 + 3 x + 1 có đồ thị là (C) không có cực trị (2).Hàm số y = x 3 + 3 x 2 + 3 x + 1 có điểm uốn là U(-1;0) (3). Đồ thị hàm số y = 3 x - 2 x - 2 có dạng.Hàm số y = 2 x + 1 x + 1 có lim x → 1 + 2 x + 1 x + 1 = - ∞ và lim x → 1 - 2 x + 1 x + 1 = + ∞ .Số các phát biểu đúng là:
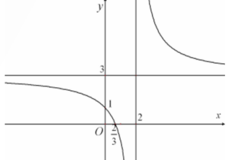
A. 1
B. 2
C. 3
D. 0
Cho hàm số y = -\(\dfrac{3}{2}\)x\(^2\) có đồ thị (P) và y = -2x + \(\dfrac{1}{2}\) có đồ thị (d)
1/ Vẽ (P) và (d) trên cùng một hệ trục tọa độ vuông góc. Xác định tọa độ các giao điểm của (P) và (d).
2/ Tìm tọa độ những điểm trên (P) thỏa tính chât tổng hoành độ và tung độ của điểm đó bằng -4.
Cho hàm số y = 2 x + 1 2 x - m có đồ thị (C) và hai điểm A ( -2;3 ); C ( 4;1 ) . Tìm m để đường thẳng d : 3 x - y - 1 = 0 cắt đồ thị (C) tại hai điểm phân biệt B, D sao cho tứ giác ABCD là hình thoi
A. 8 3
B. 3 8
C. 4 3
D. 3 4
Đường thẳng AC qua A ( -2;3 ); C ( 4;1 ) nhận A C → = 6 ; - 2 làm vec tơ chỉ phương nên có phương trình là: x + 2 6 = y - 3 - 2 ⇔ y = - 1 3 x + 7 3
Tọa độ giao điểm của AC và BD là nghiệm của hệ phương trình 3 x - y - 1 = 0 y = - 1 3 x + 7 3 ⇔ x = 1 y = 2
Để ý rằng A C ⊥ B D và I là trung điểm AC.
Khi đó ABCD là hình thoi thì I ( 1;2 ) là trung điểm của BD.
Phương trình hoành độ giao điểm của (C) và d là: 2 x + 1 2 x - m = 3 x - 1 ⇔ 6 x 2 - 3 m + 4 x + m - 1 = 0
Do ∆ = 3 m + 4 2 - 4 . 6 m - 1 = 9 m 2 + 24 > 0 , ∀ m nên d luôn cắt (C) tại hai điểm phân biệt B và D.
Gọi x 1 , x 2 là hai nghiệm của phương trình (*). Theo định lý Viet ta có x 1 + x 2 2 = 3 m + 4 12
Đáp án A
Để I là trung điểm của BD thì 3 m + 4 12 = 1 ⇔ m = 8 3
Đáp án A
y = 1 /2 x − 2 (d)
a)vẽ đồ thị hà số trên mặt phẳng tòa độ OX
b)Tìm tòa độ giao điểm E của đường thẳng (d)và(d'): y= -2x+3
c)hãy tìm m để đồ thị hàm số y=(m-2)x+m và 2 đừng thẳng (d)và(d') đồng quy
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}\dfrac{1}{2}x-2=-2x+3\\y=-2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\cdot\dfrac{5}{2}=5\\y=-2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-1\end{matrix}\right.\)
Cho hàm số y=2x+m (d)
1)Tìm m để đồ thị hàm số (d) đi qua:
a)A(-1;3)
b)B(\(\sqrt{2}\);\(-5\sqrt{2}\))
2)Tìm m để đồ thị hàm số (d) cắt đồ thị hàm số y=3x-2 trong góc phần tư thứ tư
a: Thay x=1 và y=3 vào (d), ta được:
m+2=3
hay m=1
Bài 1:
a. Để $(d)$ đi qua $A(-1;3)$ thì:
$y_A=2x_A+m\Leftrightarrow 3=2(-1)+m$
$\Leftrightarrow m=5$
b. Để $(d)$ đi qua $B(\sqrt{2}; -5\sqrt{2})$ thì:
$y_B=2x_B+m$
$\Leftrightarrow -5\sqrt{2}=2\sqrt{2}+m$
$\Leftrightarrow m=-7\sqrt{2}$
Bài 2:
PT hoành độ giao điểm:
$2x+m=3x-2$
$\Leftrightarrow m+2=x$
$y=3x-2=3(m+2)-2=3m+4$
Vậy tọa độ của 2 đths là $(m+2, 3m+4)$
Để 2 đths cắt nhau tại góc phần tư thứ nhất thì \(\left\{\begin{matrix} m+2>0\\ 3m+4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m>-2\\ m> \frac{-4}{3}\end{matrix}\right.\Leftrightarrow m> \frac{-4}{3}\)