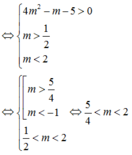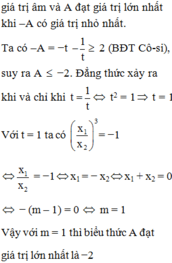tìm giá trị lớn nhất của tham số m để f(x)=x2-2(m+1)x+m2+2m<0 \(\forall x\in R\)

Những câu hỏi liên quan
Tìm các giá trị của tham số m để các tam thức bậc hai sau có dấu không đổi (không phụ thuộc vào x).
f
(
x
)
(
m
2
+
m
+
1
)
x
2
-
(
2
m
-
1
)
x
+
1
Đọc tiếp
Tìm các giá trị của tham số m để các tam thức bậc hai sau có dấu không đổi (không phụ thuộc vào x).
f ( x ) = ( m 2 + m + 1 ) x 2 - ( 2 m - 1 ) x + 1
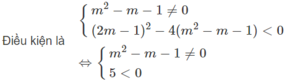
Không có giá trị nào của m thỏa mãn điều kiện này.
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
x
3
–
(
2
m
-
1
)
x
2
+
(
2
-
m
)
x
+
2
. Tìm tất cả các giá trị thực của tham số m để hàm số yf(|x|) có 5 cực trị A.
-
10
m
5
4
B.
-...
Đọc tiếp
Cho hàm số f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y=f(|x|) có 5 cực trị
A. - 10 < m < 5 4
B. - 2 < m < 5
C. - 2 < m < 5 4
D. 5 4 < m < 2
Tìm tất cả các giá trị của m để hàm số
f
(
x
)
-
x
3
+
(
2
m
-
1
)
x
2
-
(
m...
Đọc tiếp
Tìm tất cả các giá trị của m để hàm số f ( x ) = - x 3 + ( 2 m - 1 ) x 2 - ( m 2 + 8 ) x + 2 đạt cực tiểu tại x=-1.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. Không tìm được ![]() .
.
Chọn D
![]() .
.
Hàm số đạt cực tiểu tại ![]()
![]()
![]() .
.
Phương trình vô nghiệm.
Vậy không tìm được ![]() thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Bài 1. Cho hàm số: y 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x 1Bài 2. Cho hàm số y 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x -2 .Bài 3. Cho hàm số y 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x 2.Bài 4. Tìm tất cả tham số thực m để hàm số y (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tạix -1.Bài 5. Tìm giá trị của tham số m để hàm số y x3/3...
Đọc tiếp
Bài 1. Cho hàm số: y = 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x = 1
Bài 2. Cho hàm số y = 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x = -2 .
Bài 3. Cho hàm số y = 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
Bài 4. Tìm tất cả tham số thực m để hàm số y = (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tại
x = -1.
Bài 5. Tìm giá trị của tham số m để hàm số y = x3/3 +(2m - 1)x2 + (m - 9)x + 1 đạt cực tiểu tại
x = 2 .
Đừng hỏi tại sao tui ngu!!!
Giúp.com.vn
Cho phương trình x2-2(m+1)x+m2+2m=0 (1) , (với m là tham số ). Tìm các giá trị của m để phương trình (1) có hai nghiệm trái dấu
Để phương trình (1) có hai nghiệm trái dấu thì \(1\left(m^2+2m\right)< 0\)
\(\Leftrightarrow m^2+2m< 0\)
\(\Leftrightarrow m^2+2m+1< 1\)
\(\Leftrightarrow\left(m+1\right)^2< 1\)
\(\Leftrightarrow\left\{{}\begin{matrix}m+1>-1\\m+1< 1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-2\\m< 0\end{matrix}\right.\Leftrightarrow-2< m< 0\)
Đúng 1
Bình luận (0)
Ta có: \(\Delta'=1>0\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm phân biệt
Theo Vi-ét: \(x_1x_2=m^2+2m\)
Để phương trình có 2 nghiệm trái dấu
\(\Leftrightarrow m^2+2m< 0\) \(\Leftrightarrow-2< m< 0\)
Vậy để phương trình có 2 nghiệm trái dấu thì \(-2< m< 0\)
Đúng 1
Bình luận (0)
Tìm giá trị của tham số m để hàm số
a) y = x 3 + (m + 3) x 2 + mx – 2 đạt cực tiểu tại x = 1
b) y = −( m 2 + 6m) x 3 /3 − 2m x 2 + 3x + 1 đạt cực đại tại x = -1;
a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 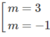
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.
Đúng 0
Bình luận (0)
Cho phương trình
x
2
– (m – 1)x –
m
2
+ m – 2 0, với m là tham số. Gọi hai nghiệm của phương trình đã cho là
x
1
;
x
2
. Tìm m để biểu thức
A
x
1
x
2...
Đọc tiếp
Cho phương trình x 2 – (m – 1)x – m 2 + m – 2 = 0, với m là tham số. Gọi hai nghiệm của phương trình đã cho là x 1 ; x 2 . Tìm m để biểu thức A = x 1 x 2 3 - x 2 x 1 3 đạt giá trị lớn nhất
A. m = 4
B. m = 3
C. m = 2
D. m = 1
Cho hàm số
f
(
x
)
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3...
Đọc tiếp
Cho hàm số
f
(
x
)
=
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3
,
với m là tham số thực.
Hàm số
g
(
x
)
=
x
2
+
4
x
+
5
x
+
2
có đồ thị C và bảng biến thiên sau:
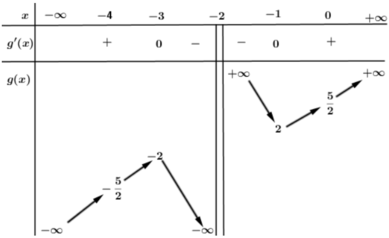
Tìm m sao cho hàm số f(x) đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn -1
A. m> 2
B. 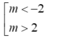
C. m < -5/2
D. m> 5 2
Xét phương trình f’ (x) = x2+(4-m) x+5-2m=0
⇔ x 2 + 4 x + 5 = m ( x + 2 ) ⇔ g ( x ) = x 2 + 4 x + 5 x + 2 = m
Ta có nghiệm của f’ (x)=0 cũng là hoành độ giao điểm của g(x)=m
Khi đó từ bảng biến thiên ta có YCBT khi m> 2.
Chọn A.
Đúng 0
Bình luận (0)
Tìm giá trị của tham số m để hàm số y = −( m 2 + 6m) x 3 /3 − 2m x 2 + 3x + 1 đạt cực đại tại x = -1
y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = − m + 1 2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − m + 1 2 + 4 = 0 ⇔ m + 1 2 = 4
⇔ 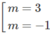
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.
Đúng 0
Bình luận (0)