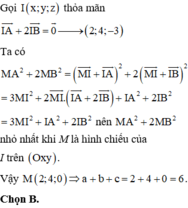Trong mp Oxy,cho 3 điểm A(3;-1),B(0;2),C(0;-4)
Dt ∆ABC bằng

Những câu hỏi liên quan
Trong không gian Oxyz, cho hai điểm
A
-
2
;
2
;
-
3
,
B
4
;
5
;
-
3
.
M
a
,
b
,
c...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A - 2 ; 2 ; - 3 , B 4 ; 5 ; - 3 . M a , b , c là điểm trên mp (Oxy) sao cho M A 2 + 2 M B 2 đạt giá trị nhỏ nhất. Tính tổng a + b + c
A. 3
B. 6
C. 1
D. -1
Trong mp với hệ tọa đô Oxy cho hai điểm A(1;-2), B(-4;5). Tìm tọa độ điểm M trên trục Oy sao cho 3 điểm M,A,B thẳng hàng
Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)
Đúng 2
Bình luận (0)
Trong mp Oxy cho điểm. A(-2;3) và đường thẳng d : x+y-3=0 tìm ảnh của A và d qua phép quay tâm O góc 90
Trong mp Oxy cho đường thẳng (P): x-2y+3=0, A(1,3), B(-1,-1). Tìm điểm M thuộc d thõa P= MA+MB là nhỏ nhất
Đường thẳng đi qua hai điểm A và B nhận \(\overrightarrow{AB}=\left(-2;-4\right)\) làm vecto chỉ phương.
Phương trình đường thẳng AB là \(\dfrac{x-1}{-2}=\dfrac{y-3}{-4}\Leftrightarrow2x-y+1=0\)
\(P=MA+MB\) đạt giá trị nhỏ nhất khi M, A, B thẳng hàng
\(\Leftrightarrow M\) là giao điểm của đường thẳng AB và d
\(\Leftrightarrow M\) có tọa độ nghiệm của hệ \(\left\{{}\begin{matrix}x-2y+3=0\\2x-y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow M\left(\dfrac{1}{3};\dfrac{5}{3}\right)\)
Đúng 1
Bình luận (0)
Trong mp Oxy, cho 4 điểm A(5;2) , B(1;-6) , C(3;- 4) và D(7;- 4). Điểm I(4;-5) là trung điểm của đoạn thẳng nào sau đây?
A. BD B. BC C. AC D. CD
trong mp tọa độ Oxy, cho đg thg d: 2x-y+3=0 và 2 điểm A(1;0); B(2;1). tìm điểm M trên d sao cho MA+MB nhỏ nhất
Thay tọa độ A và B vào d thấy kết quả cùng dấu \(\Rightarrow\) A và B nằm cùng phía so với d
Gọi C là điểm đối xứng A qua d \(\Rightarrow MA=CM\Rightarrow MA+MB=CM+MB\ge CB\)
\(\Rightarrow MA+MB\) nhỏ nhất khi M;B;C thẳng hàng hay M là giao điểm của đường thẳng BC và d
Phương trình d' qua A và vuông góc d có dạng:
\(1\left(x-1\right)+2\left(y-0\right)=0\Leftrightarrow x+2y-1=0\)
D là giao điểm d và d' \(\Rightarrow\left\{{}\begin{matrix}x+2y-1=0\\2x-y+3=0\end{matrix}\right.\) \(\Rightarrow D\left(-1;1\right)\)
C đối xứng A qua d khi và chỉ khi D là trung điểm AC \(\Rightarrow C\left(-3;1\right)\)
\(\Rightarrow\overrightarrow{CB}=\left(5;0\right)=5\left(1;0\right)\Rightarrow\) phương trình BC có dạng:
\(0\left(x-2\right)+1\left(y-1\right)=0\Leftrightarrow y-1=0\)
M là giao điểm d và BC nên tọa độ thỏa mãn: \(\left\{{}\begin{matrix}y-1=0\\2x-y+3=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{3}{2};1\right)\)
Đúng 0
Bình luận (0)
Trong không gian tọa độ Oxyz, cho hai điểm A(1;0;-3), B(3;-1;0). Viết phương trình tham số của đường thẳng d là hình chiếu vuông góc của đường thẳng AB trên mp(Oxy). A.
x
0
y
−
t
z...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho hai điểm A(1;0;-3), B(3;-1;0). Viết phương trình tham số của đường thẳng d là hình chiếu vuông góc của đường thẳng AB trên mp(Oxy).
A. x = 0 y = − t z = − 3 + 3 t
B. x = 1 + 2 t y = 0 z = − 3 + 3 t
C. x = 1 + 2 t y = − t z = 0
D. x = 0 y = 0 z = − 3 + 3 t
Đáp án C
Hình chiếu của A,B trên mp(Oxy) là A ' 1 ; 0 ; 0 ; B ' 3 ; − 1 ; 0 . Có A B → = 2 ; − 1 ; 0 là vtcp của A’B’ nên phương trình tham số của A’B’ là
x = 1 + 2 t y = − t z = 0 .
Đúng 0
Bình luận (0)
Trong không gian tọa độ Oxyz, cho hai điểm A (1;0;-3), B (3;-1;0). Viết phương trình tham số của đường thẳng d là hình chiếu vuông góc của đường thẳng AB trên mp (Oxy). A.
x
0
y
-
t...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho hai điểm A (1;0;-3), B (3;-1;0). Viết phương trình tham số của đường thẳng d là hình chiếu vuông góc của đường thẳng AB trên mp (Oxy).
A. x = 0 y = - t z = - 3 + 3 t
B. x = 1 + 2 t y = 0 z = - 3 + 3 t
C. x = 1 + 2 t y = - t z = 0
D. x = 0 y = 0 z = - 3 + 3 t
Đáp án C
Hình chiếu của A,B trên mp (Oxy) là A'(1;0;0); B'(3;-1;0). Có A B → = ( 2 ; - 1 ; 0 ) là vtcp của A’B’ nên phương trình tham số của A’B’ là
x = 1 + 2 t y = - t z = 0
Đúng 0
Bình luận (0)
trong mp Oxy cho 4 điểm A(-2;6), B(4;-4), C(2;-2) và D(-1;-3)
chứng minh ABCD là hình thang
Sửa đề: C(2;2)
\(\overrightarrow{AB}=\left(6;-10\right)\)
\(\overrightarrow{DC}=\left(-3;5\right)\)
Vì vecto AB=-2vecto DC
nên AB//DC
=>ABCD là hình thang
Đúng 0
Bình luận (0)