Để chứng minh a. ON//(SAB) và b. (OMN)//(SCD), chúng ta có thể sử dụng các định lý và quy tắc trong hình học không gian.

a. Để chứng minh ON//(SAB), ta có thể sử dụng định lý về đường thẳng song song trong hình học không gian. Theo định lý này, nếu có hai đường thẳng cắt một mặt phẳng và các đường thẳng này đều song song với một đường thẳng thứ ba trong mặt phẳng đó, thì hai đường thẳng đó cũng song song với nhau. Áp dụng định lý này, ta có thể chứng minh ON//(SAB) bằng cách chứng minh rằng ON và AB đều song song với một đường thẳng thứ ba trong mặt phẳng chứa chóp S.ABCD.

b. Để chứng minh (OMN)//(SCD), ta cũng có thể sử dụng định lý về đường thẳng song song trong hình học không gian. Tương tự như trường hợp trước, ta cần chứng minh rằng OM và CD đều song song với một đường thẳng thứ ba trong mặt phẳng chứa chóp S.ABCD.

Tuy nhiên, để chứng minh chính xác các phần a và b, cần có thêm thông tin về các góc và độ dài trong hình chóp S.ABCD.

Tự vẽ hình nhé!

Ta có:

\(V_{OBCNM}=\dfrac{1}{3}d\left(O;\left(BCNM\right)\right).S_{BCNM}=\dfrac{1}{3}.\dfrac{1}{2}d\left(A;\left(SBC\right)\right).\dfrac{3}{4}S_{SBC}=\dfrac{1}{8}V_{SABC}=\dfrac{1}{16}V_{SABCD}\)

\(\Rightarrow\dfrac{V_{OBCNM}}{V_{SABCD}}=\dfrac{1}{16}\)

Đáp án B

Dễ thấy M N | | A B nên mặt phẳng (CMN) cắt mặt phẳng (ABCD) theo giao tuyến là đường thẳng qua C và song song với AB.

Vậy giao tuyến của (MNC) và (ABD) là đường thẳng CD.

Nối AN kéo dài cắt CD tại E, nối EM kéo dài cắt SD tại I

Do N là trung điểm OB \(\Rightarrow\dfrac{BN}{ND}=\dfrac{1}{3}\)

Áp dụng định lý talet: \(\dfrac{BF}{AD}=\dfrac{BN}{ND}=\dfrac{1}{3}\) \(\Rightarrow\dfrac{CF}{AD}=\dfrac{2}{3}\)

Cũng theo Talet:

\(\dfrac{FC}{FD}=\dfrac{CF}{AD}=\dfrac{2}{3}\) \(\Rightarrow\dfrac{DF}{FC}=\dfrac{3}{2}\)

Áp dụng định lý Menelaus cho tam giác SCD:

\(\dfrac{IS}{ID}.\dfrac{DF}{FC}.\dfrac{CM}{MS}=1\Rightarrow\dfrac{IS}{ID}.\dfrac{3}{2}.1=1\Rightarrow\dfrac{IS}{ID}=\dfrac{2}{3}\)

\(\Rightarrow\dfrac{SI}{SD}=\dfrac{2}{5}\)

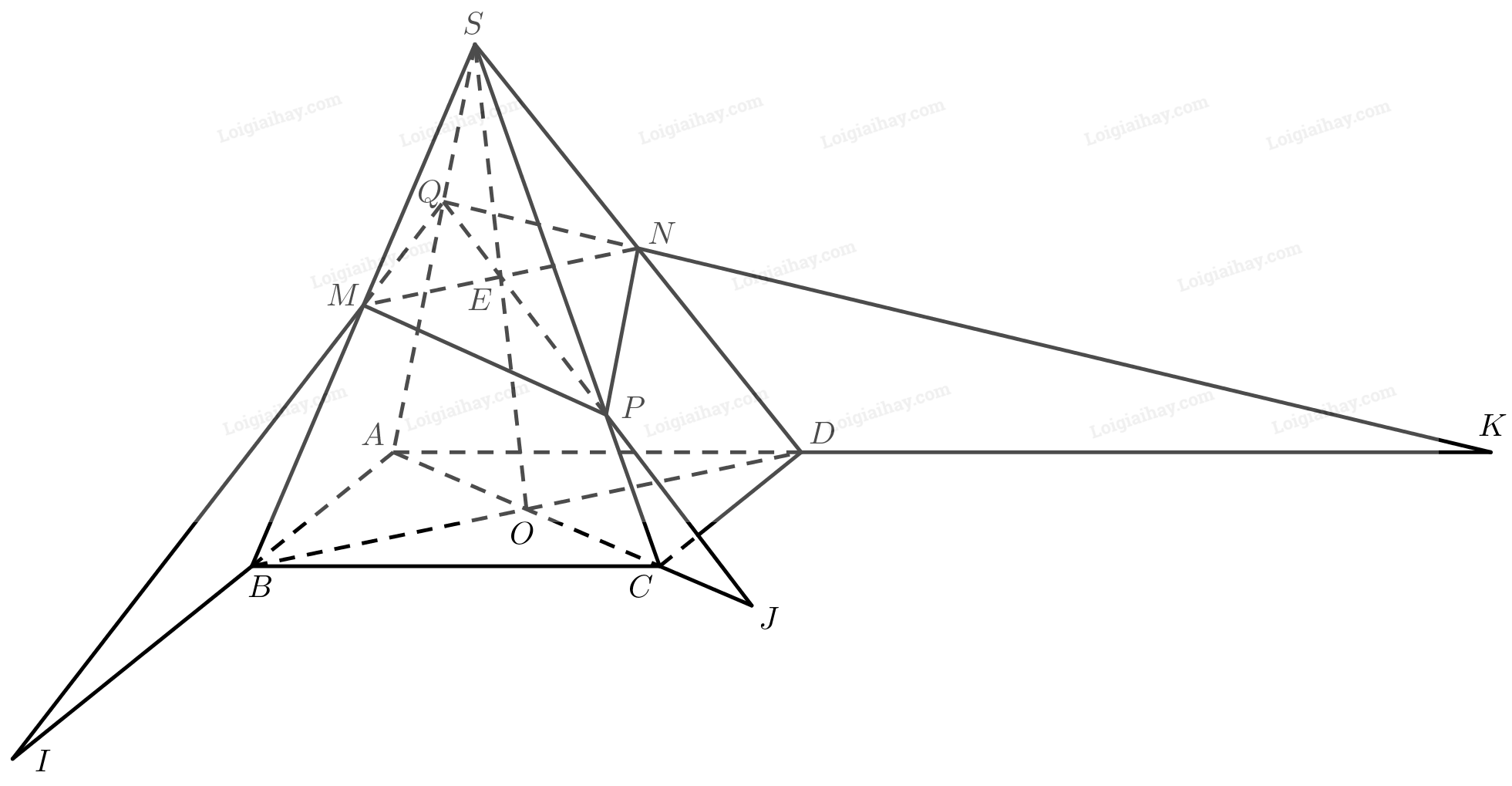
a) Gọi \(E\) là giao điểm của \(SO\) và \(MN\). Ta có:

\(\left. \begin{array}{l}E \in MN \subset \left( {MNP} \right)\\E \in S{\rm{O}}\end{array} \right\} \Rightarrow E = S{\rm{O}} \cap \left( {MNP} \right)\)

b) Gọi \(Q\) là giao điểm của \(SA\) và \(EP\). Ta có:

\(\left. \begin{array}{l}Q \in EP \subset \left( {MNP} \right)\\Q \in S{\rm{A}}\end{array} \right\} \Rightarrow Q = S{\rm{A}} \cap \left( {MNP} \right)\)

c) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}I \in QM \subset \left( {MNP} \right)\\I \in AB \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}J \in QP \subset \left( {MNP} \right)\\J \in AC \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}K \in QN \subset \left( {MNP} \right)\\K \in AD \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow K \in \left( {MNP} \right) \cap \left( {ABCD} \right)\end{array}\)

Do đó, \(I,J,K\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {ABCD} \right)\).

Vậy \(I,J,K\) thẳng hàng.

Em kiểm tra lại đề, \(\left(\alpha\right)\) đi qua AI nên nó không thể cắt SA tại M được nữa (vì nó đi qua A nên đã cắt SA tại A rồi)

Bài này ứng dụng của bài này:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfra... - Hoc24

Theo chứng minh của bài toán trên thì ta có:

\(\dfrac{SA}{SM}+\dfrac{SC}{SP}=\dfrac{SB}{SN}+\dfrac{SD}{SQ}=\dfrac{2SO}{SI}=10\)

\(\Rightarrow\dfrac{SA}{SM}+\dfrac{SB}{SN}+\dfrac{SC}{SP}+\dfrac{SD}{SQ}=20\)