Hướng dẫn (khuya quá rồi).

Trong mp (ADN), lấy Q thuộc AD sao cho \(NP||GQ\)

\(\Rightarrow\left(\overrightarrow{MG};\overrightarrow{NP}\right)=\left(\overrightarrow{MG};\overrightarrow{GQ}\right)=180^0-\widehat{MGQ}\)

Áp dụng định lý hàm cos là tính được (\(GP=\dfrac{2}{3}NP\) ; tính MQ dựa vào hàm cos tam giác AMQ)

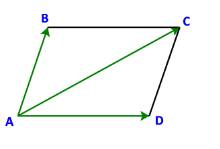
a) Ta có: \(\left\{ \begin{array}{l}AD//BC\\AD = BC\end{array} \right.\) (do tứ giác ABCD là hình bình hành)

\( \Rightarrow \overrightarrow {AD}  = \overrightarrow {BC} \)

b) Ta có: \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

Tham khảo:

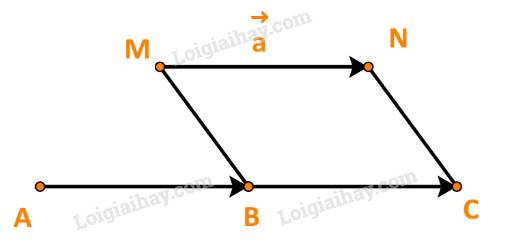
Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).

Từ B, M, N ta dựng hình bình hành BMNC.

Khi đó: \(\overrightarrow {MN}  = \overrightarrow {BC} \) hay \(\overrightarrow a  = \overrightarrow {BC} \).

\( \Rightarrow \overrightarrow a  + \overrightarrow a  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

a) Vì  \(\overrightarrow {AB}  = \overrightarrow a  = \overrightarrow {BC} \) nên A, B, C thẳng hàng và B là trung điểm của AC.

Vậy \(\overrightarrow a  + \overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng, \(\left| {\overrightarrow a  + \overrightarrow a } \right| = 2.\left| {\overrightarrow {AB} } \right|\)

b) Ta có:  \(\overrightarrow a  + \overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng, \(\left| {\overrightarrow a  + \overrightarrow a } \right| = 2.\left| {\overrightarrow {AB} } \right|\)

Mà \(\overrightarrow {AB}  = \overrightarrow a \) nên:  \(\overrightarrow a  + \overrightarrow a \) và \(\overrightarrow a \) cùng hướng, \(\left| {\overrightarrow a  + \overrightarrow a } \right| = 2.\left| {\overrightarrow a } \right|\).

\(\overrightarrow{AB}.\overrightarrow{BD}=-\overrightarrow{BA}.\overrightarrow{BD}=-a.a.cos60^0=-\dfrac{a^2}{2}\)

Từ M kẻ đường thẳng song song với AB, cắt AD tại E.

Khi đó tứ giác ABME là hình bình hành.

Do đó: \(\overrightarrow {AM}  = \overrightarrow {AB}  + \overrightarrow {AE} \).

Dễ thấy: \(AE = BM = \frac{1}{2}BC = \frac{1}{2}AD\)

\( \Rightarrow \overrightarrow {AE}  = \frac{1}{2}\overrightarrow {AD} \)

\( \Rightarrow \overrightarrow {AM}  = \overrightarrow {AB}  + \frac{1}{2}\overrightarrow {AD} \)

Vậy \(\overrightarrow {AM}  = \overrightarrow {AB}  + \frac{1}{2}\overrightarrow {AD} \)

Chú ý khi giải

+) Dựng hình hình hành sao cho đường chéo là vecto cần biểu thị, 2 cạnh của nó song song với giá của hai vecto đang biểu thị theo.

a: AB=BC=CD=DA=6a

\(AC=BD=\sqrt{\left(6a\right)^2+\left(6a\right)^2}=6a\sqrt{2}\)

\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=6a\)

\(\left|\overrightarrow{BC}+\overrightarrow{BD}\right|=\sqrt{BC^2+BD^2+2\cdot BC\cdot BD\cdot cos45}\)

\(=\sqrt{36a^2+72a^2+\sqrt{2}\cdot6a\cdot6a\sqrt{2}}\)

\(=6a\sqrt{5}\)

b: \(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=6a\cdot6a\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}\)

\(=36a^2\)

\(cos\left(\overrightarrow{b};\overrightarrow{a}-\overrightarrow{b}\right)=\dfrac{\overrightarrow{b}\left(\overrightarrow{a}-\overrightarrow{b}\right)}{\left|\overrightarrow{b}\right|.\left|\overrightarrow{a}-\overrightarrow{b}\right|}=\dfrac{\overrightarrow{a}.\overrightarrow{b}-\overrightarrow{b}^2}{1.\sqrt{3}}=\dfrac{2.1.cos\dfrac{\pi}{3}-1^2}{\sqrt{3}}=0\)

\(\Rightarrow\left(\overrightarrow{b};\overrightarrow{a}-\overrightarrow{b}\right)=90^0\)