Xác định hàm số y=g(x)=(a+2).x2+2a-1 biết g(2)=19
Những câu hỏi liên quan
Cho hàm số
y
f
x
2
x
3
-
7
x
+
6
x
-
2...
Đọc tiếp
Cho hàm số y = f x = 2 x 3 - 7 x + 6 x - 2 k h i x < 2 a + 1 - x 2 + x k h i x ≥ 2 . Xác định a để hàm số f(x) liên tục tại x = 2 .
Cho hàm số
f
x
x
2
+
x
−
6
x
−
2
k...
Đọc tiếp
Cho hàm số f x = x 2 + x − 6 x − 2 k h i x > 2 − 2 a x + 1 k h i x ≤ 2 . Xác định a để hàm số liên tục tại điểm x = 2
A. a = 2
B. a = 1 2
C. a = 1
D. a = − 1
Đáp án D
Để hàm số liên tục tại điểm x = 2 thì lim x → 2 + f x = f 2
Ta có
lim x → 2 + f x = lim x → 2 + x 2 + x − 6 x − 2 = lim x → 2 + x − 2 x + 3 x − 2 = lim x → 2 + x + 3 = 5
lim x → 2 − f x = lim x → 2 − − 2 a x + 1 = − 4 a + 1 ; f 2 = − 4 a + 1
Do đó để hàm số liên tục thì
− 4 a + 1 = 5 ⇔ a = − 1.
Đúng 0
Bình luận (0)
Cho hàm số
f
x
x
2
+
x
−
6
x
−
2
k...
Đọc tiếp
Cho hàm số f x = x 2 + x − 6 x − 2 k h i x > 2 − 2 a x + 1 k h i x ≤ 2 . Xác định a để hàm số liên tục tại điểm x = 2
A. a = 2
B. a = 1 2
C. a = 1
D. a = -1
Cho hàm số yf(x) xác định và liên tục trên R, có đồ thị hàm số yf’(x) như hình vẽ bên dưới. Hàm số g(x)f(x) – 1/2 x2+ x-8 có bao nhiêu điểm cực tiểu? A. 3 B. 2 C. 1. D. 4
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên R, có đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Hàm số g(x)=f(x) – 1/2 x2+ x-8 có bao nhiêu điểm cực tiểu?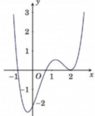
A. 3
B. 2
C. 1.
D. 4
Cho hàm số y=f(x) liên tục trên R có đồ thị y=f '(x) như hình vẽ:
a)Tìm min, max của hàm số g(x)=f(\(\sqrt{8-x^2-2x}-1\))
b)Xác định khoảng đb, nb, cực đại, cực tiểu của g(x)=f(x2+x)
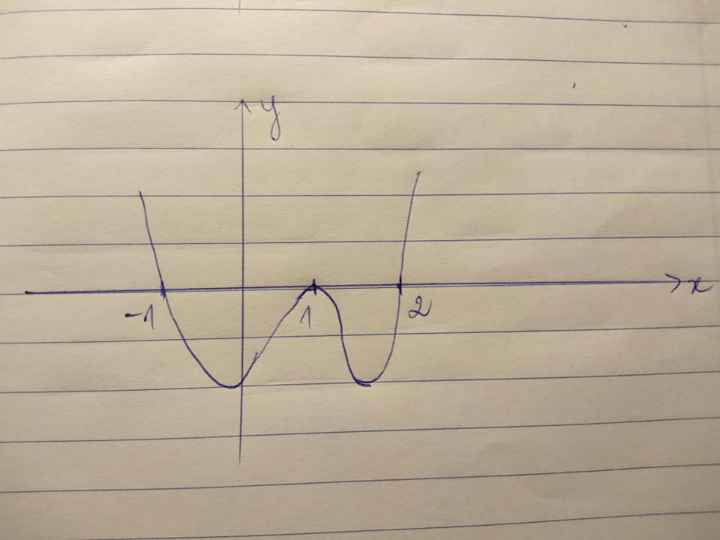
a.
TXĐ: \(D=\left[-4;2\right]\)
\(0\le\sqrt{9-\left(x+1\right)^2}\le3\Rightarrow-1\le\sqrt{9-\left(x+1\right)^2}\le2\)
\(\Rightarrow f'\left(\sqrt{8-x^2-2x}-1\right)\le0\) ; \(\forall x\in D\)
\(g'\left(x\right)=-\dfrac{x+1}{\sqrt{8-x^2-2x}}.f'\left(\sqrt{8-x^2-2x}-1\right)\) luôn cùng dấu \(x+1\)
\(\Rightarrow g\left(x\right)\) đồng biến trên \(\left[-1;2\right]\) và nghịch biến trên \(\left[-4;-1\right]\)
Từ BBT ta thấy \(g\left(x\right)_{max}=g\left(-4\right)=g\left(2\right)=f\left(-1\right)=?\)
\(g\left(x\right)_{min}=g\left(-1\right)=f\left(2\right)=?\)
(Do đề chỉ có thế này nên ko thể xác định cụ thể được min-max)
b.
\(g'\left(x\right)=\left(2x+1\right).f'\left(x^2+x\right)=0\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\f'\left(x^2+x\right)=0\left(1\right)\end{matrix}\right.\)
Xét (1), ta chỉ cần quan tâm 2 nghiệm bội lẻ:
\(f'\left(x^2+x\right)=0\Rightarrow\left[{}\begin{matrix}x^2+x=-1\left(vô-nghiệm\right)\\x^2+x=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Với \(\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\) \(\Rightarrow x^2+x\ge2\) ; với \(-2\le x\le1\Rightarrow-1\le x^2+x\le2\) nên ta có bảng xét dấu:
Từ BBT ta có: \(x=-\dfrac{1}{2}\) là cực đại, \(x=-2;x=1\) là 2 cực tiểu
Hàm đồng biến trên ... bạn tự kết luận
Đúng 1
Bình luận (0)
Bài 3: Vẽ trên cùng một hệ trục tọa độ Oxy đồ thị của hàm số y=3x và y= -1/x
Bài 4: Xác định hệ số a của hàm số y=ax, biết đồ thị của nó đi qua điểm A (1;2)
Bài 5: Xác định hệ số a của hàm số y=( 2a +1), biết đồ thị của nó đi qua điểm A (1;2)
Các bạn giúp mình nha, mai mình học rùi
Bài 4:
Thay x=1 và y=2 vào y=ax, ta được:
a=2
Đúng 1
Bình luận (0)
cho hàm số y = f ( x ) = ax
a , Xác định đồ thị hàm số biết đồ thị của hàm số đi qua điểm ( 3 , - 42)
b Cho hàm số y = g(x) = 100- 3 . x3
Tính g(-2 ) ; g( 3 )
a: Thay x=3 và y=-42 vào y=ax, ta được:
3a=-42
hay a=-14
Đúng 1
Bình luận (1)
Cho hàm số f(x) xác định và liên tục trên R. Gọi g(x) là một nguyên hàm của y
x
x
+
f
2
(
x
)
hàm số Biết rằng
∫
1
2
g
(
x
)
d
x
1
và 2g(2)-g(1)2 Tích phân
∫...
Đọc tiếp
Cho hàm số f(x) xác định và liên tục trên R. Gọi g(x) là một nguyên hàm của y= x x + f 2 ( x ) hàm số Biết rằng ∫ 1 2 g ( x ) d x = 1 và 2g(2)-g(1)=2 Tích phân
∫ 1 2 x 2 x + f 2 ( x ) d x bằng
A. 1,5
B. 1
C. 3
D. 2
Chọn đáp án B.
Vì g(x) là một nguyên hàm của hàm số
Đúng 0
Bình luận (0)
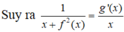
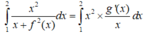
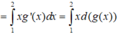
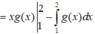
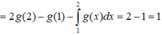
Cho y = (2a-5)x+a-2 (d)
a. Tìm a để (d) là hàm số bậc nhất
b. Xác định (d) biết (d) vuông góc y=3x+4
c. Xác định (d) biết (d) // y=-2x+5
d. Xác định (d) biết (d) cắt oy tại -2 và cắt ox tại \(\sqrt{3}\)
a: Để (d) là hàm số bậc nhất thì 2a-5<>0
hay\(a\ne\dfrac{5}{2}\)
b:Vì (d) vuông góc với 3x+4
nên 3(2a-5)=-1
\(\Leftrightarrow2a-5=-\dfrac{1}{3}\)
\(\Leftrightarrow2a=5-\dfrac{1}{3}=\dfrac{14}{3}\)
hay \(a=\dfrac{7}{3}\)
Đúng 2
Bình luận (0)
a) 2a - 5 # 0 <=> a # 5/2
b) (2a - 5).3 = -1
<=> a = 7/3 (thỏa a#5/2)
c) 2a - 5 = -2 và a - 2 # 5
<=> a = 3/2
Đúng 1
Bình luận (0)