A đúng, trục hoành nhận mọi vecto có dạng \(\left(0;k\right)\) với \(k\ne0\) là vtpt

a,Vuông tại A mới đúng

 \(AB=2\sqrt{10};AC=\sqrt{10};BC=5\sqrt{2}\)

\(\Rightarrow AB^2+AC^2=40+10=50=BC^2\)

\(\Rightarrow\Delta ABC\) vuông tại A

b, \(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC.sinA=\dfrac{1}{2}.2\sqrt{10}.\sqrt{10}.sin90^o=10\)

c, \(D\left(0;y_0\right)\)

\(A;C;D\) thẳng hàng \(\Leftrightarrow\overrightarrow{AC}=k.\overrightarrow{AD}\)

\(\Leftrightarrow\left\{{}\begin{matrix}3=k\\-1=k\left(y_0-4\right)\end{matrix}\right.\Rightarrow y_0=\dfrac{11}{3}\)

\(\Rightarrow D\left(0;\dfrac{11}{3}\right)\)

a: Vì hệ số góc là -3 nên a=-3

Vậy: (d): y=-3x+b

THay x=-1 và y=2 vào (d), ta được: b+3=2

hay b=-1

a: Vì (d) có hệ số góc là -3 nên a=-3

Vậy: (d): y=-3x+b

Thay x=-1 và y=2 vào (d), ta được:

b+3=2

hay b=-1

\(a,\) Gọi \(\left(d\right):y=ax+b\left(a\ne0\right)\) là đt cần tìm

\(\Leftrightarrow\left\{{}\begin{matrix}-a+b=2\\a=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=-1\end{matrix}\right.\Leftrightarrow\left(d\right):y=-3x-1\)

\(b,\) Gọi \(\left(d_1\right):y=ax+b\left(a\ne0\right)\) là đt cần tìm

\(\Leftrightarrow\left\{{}\begin{matrix}2a+b=3\\4a+b=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\Leftrightarrow\left(d_1\right):y=x+1\)

\(c,PTHDGD:-3x-1=x+1\Leftrightarrow x=-\dfrac{1}{2}\Leftrightarrow y=\dfrac{1}{2}\Leftrightarrow B\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\\ \text{Vậy }B\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\text{ là giao 2 đths}\)

AB=(3;-1)

AC=(4;2)

AB.AC= |AB|.|AC|.cos(AB,AC)

cos( AB,AC)= \(\dfrac{10}{\sqrt{10}.2\sqrt{5}}=\dfrac{\sqrt{2}}{2}\)

BAC=45

Đáp án là D

Chọn B

Gọi  là vectơ pháp tuyến của (P) thỏa yêu cầu bài toán.

(P) qua N (-1; 0; -1) nên phương trình mặt phẳng có dạng:

A(x+1) + By + C(z+1) = 0 <=> Ax + By + Cz + A + C = 0

• (P) qua M (1;2;1) suy ra

A + 2B + C + A + C = 0 <=> A + B + C = 0 => A + C = - B (1)

• (P) cắt trục Ox tại A(a; 0; 0) suy ra A.a + A + C = 0 => A.a - B = 0 => a = B/A

(Do nếu A = 0 => B = 0 => C = 0 nên A ≠ 0). Suy ra A(B/A; 0; 0)

• (P) cắt trục Oy tại B (0; b; 0) suy ra B.b + A + C = 0 => B.b - B = 0 => B = 0 hoặc b = 1

TH1: B = 0 => A + C = 0. Chọn C = 1 => A = -1

Phương trình mặt phẳng (P) có dạng: x - z = 0 => A ≡ B ≡ O (0;0;0) => không thỏa yêu cầu.

TH2: b = 1 => B (0;1;0), 

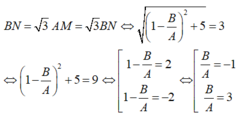
· B/A = -1 => B = -A => C = 0. Chọn A = 1 => B = -1

Phương trình mp (P): x - y + 1 = 0

· B/A = 3 => B = 3A => C = -4A. Chọn A = 1 => B = 3 => C = -4.

Phương trình mp (P): x + 3y - 4z - 3 = 0

Vậy có hai mặt phẳng thỏa yêu cầu.

- Gọi tọa độ điểm P ( x; y )

\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{PA}=\left(1-x;4-y\right)\\\overrightarrow{PB}=\left(6-x;-1-y\right)\end{matrix}\right.\)

Mà \(\overrightarrow{PA}=\dfrac{1}{3}\overrightarrow{PB}\)

\(\Rightarrow\left\{{}\begin{matrix}1-x=\dfrac{1}{3}\left(6-x\right)\\4-y=\dfrac{1}{3}\left(-1-y\right)\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=\dfrac{13}{2}\end{matrix}\right.\)

Vậy tọa độ của điểm P thỏa mãn là : \(P\left(-\dfrac{3}{2};\dfrac{13}{2}\right)\)