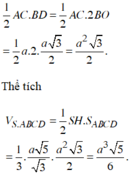Cho khối chóp S . A B C D có đáy A B C D là hình thoi cạnh a, S A = S B = S C = a , cạnh SD thay đổi. Thể tích lớn nhất của khối chóp S . A B C D bằng
A. a 3 8
B. a 3 2
C. 3 a 3 8
D. a 3 4
Những câu hỏi liên quan
cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a góc abc=60• .SA vuông góc với mặt phẳng đáy. Tính:
a) d(A; (SBD))
b) d(C; (SAB))
Xem chi tiết
Đề thiếu dữ liệu để xác định độ dài SA rồi bạn
Đúng 0
Bình luận (0)
SGK Chân trời sáng tạo
20 tháng 8 2023 lúc 20:38
Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) cạnh \(a\). Cho biết \(SA = a\sqrt 3 ,SA \bot AB\) và \(SA \bot A{\rm{D}}\). Tính góc giữa \(SB\) và \(C{\rm{D}}\), \(S{\rm{D}}\) và \(C{\rm{B}}\).
THAM KHẢO:
CD//AB nên góc giữa SB và CD là góc giữa AB và SB, \(\widehat{ABS}\)
CB//AD nên góc giữa SD và CB là góc giữa SD và AD, \(\widehat{ADS}\)
Ta có: tan\(\widehat{ABS}\)=tan\(\widehat{ADS}\)=\(\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
Suy ra \(\widehat{ABS}\)=\(\widehat{ADS}\)=\(\dfrac{\pi}{3}\)
Đúng 1
Bình luận (0)
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA a
2
. Một mặt phẳng đi qua A vuông góc với SC cắt SB, SD, SC lần lượt tại B, D, C. Thể tích khối chóp S. ABCD là: A. V
2
a
3
3
9
B. V
2
a...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = a 2 . Một mặt phẳng đi qua A vuông góc với SC cắt SB, SD, SC lần lượt tại B', D', C'. Thể tích khối chóp S. AB'C'D' là:
A. V = 2 a 3 3 9
B. V = 2 a 3 2 3
C. V = a 3 2 9
D. V = 2 a 3 3 3
Chọn C
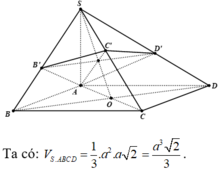
Dựa vào giả thiết ta có B', C', D' lần lượt là hình chiếu của A lên SB, SC, SD.
Tam giác SAC vuông cân tại A nên C' là trung điểm của SC.
Trong tam giác vuông SAB' ta có:
Đúng 0
Bình luận (0)
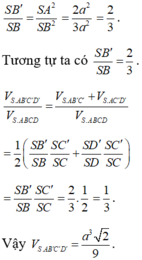
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật cạnh a, S A ⊥ (A B C D) ,SC tạo với mặt đáy một góc 60 độ và (SAB ) một góc a với sin a = căn 3/ 4 . Tính chiều cao khối chóp.
Đáy là hình vuông hay chữ nhật bạn? Hình chữ nhật sao có các cạnh bằng nhau và bằng a được?
Đúng 0
Bình luận (0)
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a
A
B
C
^
60
0
, cạnh bên SA vuông góc với đáy SA
a
3
Tính thể tích của khối chóp S. ABCD A.
a
3
4
B.
a...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a A B C ^ = 60 0 , cạnh bên SA vuông góc với đáy SA = a 3 Tính thể tích của khối chóp S. ABCD
A. a 3 4
B. a 3 3 6
C. a 3 2
D. a 3 3 3
Cho hình chóp S ABCD . có đáy là hình thoi cạnh a, hình chiếu vuông góc của S trên mặt
phẳng ABCD là trung điểm cạnh = AB ABD=60 và SC hợp với đáy một góc 0 60 . Tính
thể tích V của khối chóp S ABCD
Gọi H là trung điểm AB \(\Rightarrow SH\perp\left(ABCD\right)\)
\(\Rightarrow\) CH là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCH}=60^0\)
Do \(\widehat{ABD}=60^0\Rightarrow\) các tam giác ABD và BCD là tam giác đều cạnh a
\(\Rightarrow\widehat{ABC}=120^0\)
Áp dụng định lý hàm cos cho tam giác BCH:
\(CH=\sqrt{BC^2+BH^2-2BC.BH.cos120^0}=\dfrac{a\sqrt{7}}{2}\)
\(\Rightarrow SH=CH.tan60^0=\dfrac{a\sqrt{21}}{2}\)
\(V=\dfrac{1}{3}SH.2S_{ABD}=\dfrac{1}{3}.\dfrac{a\sqrt{21}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{7}}{8}\)
Đúng 0
Bình luận (0)
Cho hình chóp S ABCD . có đáy ABCD là hình thoi cạnh 2a, SA a 5 ; góc BCD 60 o và SA vuông góc với ( ) ABCD . Gọi K là trung điểm của CD. Tính góc giữa đường thẳng SK và ( SAB ).A. 450 . B. 300 . C. 600 . D. arctan dfrac{sqrt{7}}{sqrt{5}}help me
Đọc tiếp
Cho hình chóp S ABCD . có đáy ABCD là hình thoi cạnh 2a, SA a = 5 ; góc BCD = 60 o và SA vuông góc với ( ) ABCD . Gọi K là trung điểm của CD. Tính góc giữa đường thẳng SK và ( SAB ).
A. 450 . B. 300 . C. 600 . D. arctan \(\dfrac{\sqrt{7}}{\sqrt{5}}\)
help me
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB a, cạnh đáy CD 2a, AD a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng
3
a
2
2
. Thể tích của hình chóp S.ABCD bằng:A.
a
3
B.
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.
Đúng 0
Bình luận (0)
Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O cạnh a, góc
B
C
A
^
30
0
;
S
O
3
a
4
, Khi đó thể tích của khối chóp là A.
a...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O cạnh a, góc B C A ^ = 30 0 ; S O = 3 a 4 , Khi đó thể tích của khối chóp là
A. a 3 2 4
B. a 3 3 8
C. a 3 2 8
D. a 3 3 4
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a, ABC
60
o
,SA SB SC
a
2
Tính thể tích V của khối chóp đã cho.
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a, ABC = 60 o ,SA = SB = SC = a 2 Tính thể tích V của khối chóp đã cho.
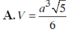
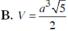
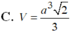
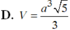
Chọn A
Phương pháp:
+ Xác định chiều cao của hình chóp bằng cách sử dụng: Nếu SA = SB = SC thì S thuộc trục đường tròn ngoại tiếp tam giác ABC hay chân đường cao hạ từ S xuống (ABC) trùng với tâm đường tròn ngoại tiếp
tam giác . ABC
+ Tính chiều cao SH dựa vào định lý Pyatgo
+ Tính thể tích theo công thức 
với h là chiều cao hình chóp, S là diện tích đáy.
Cách giải:
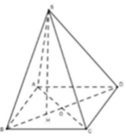
Vì ABCD là hình thoi nên AB = BC mà 
nên ABC là
tam giác đều cạnh a.
Gọi H là trọng tâm tam giác ABC, O là giao điểm hai đường chéo hình thoi.
Vì SA = SB = SC nên S thuộc trục đường tròn ngoại tiếp tam giác ABC hay chân đường cao hạ từ S xuống (ABC) trùng với tâm đường tròn ngoại tiếp H của tam giác ABC. Hay
+ Vì ABC đều cạnh a tâm H nên
Đúng 0
Bình luận (0)