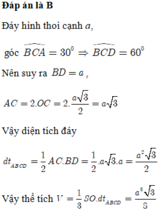Các câu hỏi tương tự
Bài 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a * sqrt(3) . O là tâm hình vuông 1/ Chứng minh :a) (SAC) I (ABCD) b) (SAC) (SBD). 2 / a ) Tính d(S; (ABCD)) b) Tính d(O; (SCD)) 3/ Tính góc giữa:a) SC và (ABCD); b) (SAB) và (ABCD).
8 tháng 6 2021 lúc 21:13
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, góc BAD = 60 ° với AC cắt BD tại O, SO ⊥ ( ABCD ) và SO = 3a/4. Tính thể tích khối chóp S.ABCD.
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a
A
B
C
^
60
0
, cạnh bên SA vuông góc với đáy SA
a
3
Tính thể tích của khối chóp S. ABCD A.
a
3
4
B.
a...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a A B C ^ = 60 0 , cạnh bên SA vuông góc với đáy SA = a 3 Tính thể tích của khối chóp S. ABCD
A. a 3 4
B. a 3 3 6
C. a 3 2
D. a 3 3 3
27 tháng 4 2021 lúc 19:30
Cho hình chóp SABCD đáy là hình vuông tâm O cạnh a. SA=a căn 3. SA vuông góc với đáy. Tính góc a)(SBD) và (ABCD) b)(SBD) và (SAB) c)(SBC) và (ABCD) d)(SCD) và (ABCD)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh bằng a,
A
B
C
^
60
0
, SASBSC, SD 2a. Gọi (P) là mặt phẳng qua A và vuông góc với SB tại K. Mặt phẳng (P) chia khối chóp S.ABCD thành hai phần có thể tích
V
1
;
V
2
trong đó...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh bằng a, A B C ^ = 60 0 , SA=SB=SC, SD= 2a. Gọi (P) là mặt phẳng qua A và vuông góc với SB tại K. Mặt phẳng (P) chia khối chóp S.ABCD thành hai phần có thể tích V 1 ; V 2 trong đó V 1 là thể tích khối đa diện chứa đỉnh S. Tính V 1 V 2
A. 11
B. 7
C. 9
D. 4
1 tháng 6 2021 lúc 20:54
Cho hình chóp SABCD đáy là hình thoi cạnh a tâm O góc BAD=60°. H là trung điểm của OB. SH vuông góc (ABCD). SH=a căn 3 phần 2. Tính khoảng cách từ AB đến SC
1 tháng 6 2021 lúc 9:20
Cho hình chóp SABCD đáy là hình thoi cạnh a tâm O góc BAD=60°. H là trung điểm của OB. SH vuông góc (ABCD). SH=a căn 3 phần 2. Tính khoảng cách từ AB đến SC
Bài 3 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M, N là trung điểm cạnh SC; SD
a) CMR: MN // (SAB); MM // (ABCD)
b) CMR: MO // (SAB)
Bài 4 :Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M,N, P là trung điểm cạnh SA, SB, SC.
a) Chứng minh rằng : MN // (SCD).
b) Chứng minh rằng: MO // (SAB)
Giúp vs bạn !!
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SASBSCSDa√2; O là tâm của hình vuông ABCD.a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD). b) C/m (SAC) ⊥(SBD)c) Tính khoảg cách từ S đến (ABCD)d) Tính góc giữa đường SB và (ABCD).e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCDf) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)g) Tính khoảng cách giữa SM và BC; SM và AB.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA=SB=SC=SD=a√2; O là tâm của hình vuông ABCD.
a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD).
b) C/m (SAC) ⊥(SBD)
c) Tính khoảg cách từ S đến (ABCD)
d) Tính góc giữa đường SB và (ABCD).
e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCD
f) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)
g) Tính khoảng cách giữa SM và BC; SM và AB.