Cho tam giác ABC có đường cao AH.Gọi I là trung điểm cạnh AC lấy điểm D đối xứng với H qua I.Chứng minh tứ giác ADCH là hình chữ nhật

Những câu hỏi liên quan
Cho tam giác ABC cân tại A,đường cao AH.Gọi I là trung điểm AC.Lấy điểm D đối xứng với với điểm H qua điểm I
a)Chứng minh tứ giác ADCH là hình chữ nhật
b)Chứng minh tứ giác ADHB là hình bình hành
c)Gọi E là trung điểm của đoạn thằng AB.Chứng minh điểm A đối xứng với điểm H qua đường thằng EI
a: Xét tứ giác ADCH có
I là trung điểm cuả AC
I là trung điểm của HD
Do đó: ADCH là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên ADCH là hình chữ nhật
Đúng 3
Bình luận (0)
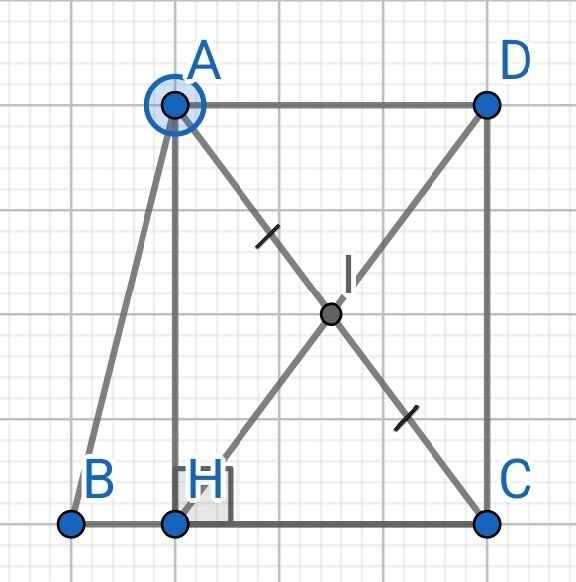
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC. Lấy D là điểm đối xứng với H qua I. Chứng minh tứ giác AHCD là hình chữ nhật.
 Do D và H đối xứng nhau qua I (gt)
Do D và H đối xứng nhau qua I (gt)
⇒ I là trung điểm của DH
Do AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
⇒ ∠AHC = 90⁰
Tứ giác AHCD có:
I là trung điểm của AC (gt)
I là trung điểm của DH (cmt)
⇒ AHCD là hình bình hành
Mà ∠AHC = 90⁰ (cmt)
⇒ AHCD là hình chữ nhật
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (AB AC). Kẻ đường cao AH (H thuộc BC). Gọi M là trung điểm của AC. Trên tia đối của tia MH lấy điểm D sao cho MD MH.a) Chứng minh tứ giác ADCH là hình chữ nhậtb) Gọi E là điểm đối xứng của C qua H. Chứng minh tứ giác ADHE là hình bình hànhc) Vẽ EK vuông góc với AB tại K. Gọi I là trung điểm của AK. Chứng minh KE // IHd) Gọi N là trung điểm của BE. Chứng minh HK vuông góc KN
Đọc tiếp
Cho tam giác ABC vuông tại A (AB > AC). Kẻ đường cao AH (H thuộc BC). Gọi M là trung điểm của AC. Trên tia đối của tia MH lấy điểm D sao cho MD = MH.
a) Chứng minh tứ giác ADCH là hình chữ nhật
b) Gọi E là điểm đối xứng của C qua H. Chứng minh tứ giác ADHE là hình bình hành
c) Vẽ EK vuông góc với AB tại K. Gọi I là trung điểm của AK. Chứng minh KE // IH
d) Gọi N là trung điểm của BE. Chứng minh HK vuông góc KN
a: Xét tứ giác ADCH có
M là trung điểm chung của AC và HD
góc AHC=90 độ
Do đó: ADCH là hình chữ nhật
b: Xét tứ giác ADHE có
AD//HE
AD=HE
Do đó: ADHE là hình bình hành
Đúng 0
Bình luận (0)
Bài 1. Cho tam giác ABC , đường cao AH . Gọi I là trung điểm của AC . Lấy D là điểm đối xứng với H qua I . Chứng minh tứ giác AHCD là hình chữ nhật
Xét tứ giác AHCD có
I là trung điểm chung của AC và HD
=>AHCD là hình bình hành
Hình bình hành AHCD có \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
Đúng 2
Bình luận (0)
+)Xét tứ giác AHCD có :
I là trung điểm chung của AC và HD
=>AHCD là hình bình hành
+)Hình bình hành AHCD có góc AHC = 90độ
=> AHCD là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, đường cao AH. Gọi H là trung điểm của AC. Lấy điểm D đối xứng với điểm H qua điểm I
a) CM tứ giác ADCH là hình chữ nhật
b) CM tứ giác ADHB là hình bình hành
c) Gọi E là trung điểm của đoạn thẳng AB. CM điểm A đối xứng với điểm H qua đường thẳng EI
d) Gọi giao điểm của BD và AC là F. Chứng minh AF= \(\frac{1}{3}\)AC
cho tam giác ABC cân tại A, đường trung tuyến AH.Gọi O là trung điểm của AC,D là điểm đối xứng với H qua O
a) Chứng minh tứ giác AHKC là hình chữ nhật
b) Tứ giác ABHD là hình gì? Tại sao?
a:
Sửa đề: Chứng minh AHCD là hình chữ nhật
ΔABC cân tại A
mà AH là đường trung tuyến
nên AH\(\perp\)BC tại H
Xét tứ giác AHCD có
O là trung điểm chung của AC và HD
=>AHCD là hình bình hành
Hình bình hành AHCD có \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
b: AHCD là hình bình hành
=>AD//HC và AD=HC
AD//HC
H\(\in\)BC
Do đó: AD//HB
AD=HC
HC=HB
Do đó: AD=HB
Xét tứ giác ABHD có
AD=HB
AD//HB
Do đó: ABHD là hình bình hành
Đúng 2
Bình luận (0)
Cho tam giác ABC nhọn (AB<AC),đường cao AH.Gọi D lần lượt là trung điểm AB,AC.Lấy điểm F đối xứng H qua I
a) Chứng minh tứ giác BFAF là hình chữ nhật
b) Đường thẳng qua B song song AC cắt DI tại E.Chứng minh tứ giác BEAD là hình gì?vì sao?
c) trên tia AC lấy O sao cho C là trung điểm AO.Gọi M là trung điểm của BH.Chứng minh OH vuông góc với AM
Nguyễn Thị Tuyết Nhung
đề cmnr viết lại cái
Bài 1:Cho tam giác ABC vuông tại A,đường cao AH.Gọi D là là điểm đối xứng với H qua AB M là giao điểm của AB và DH. Gọi E là đối xứng với H qua AC ,N là giao điểm của AC và HE.a)Chứng minh tứ giác AMHN là hình chữ nhật b)Chứng minh rằng D đối xứng với E qua Ac) Tìm điều kiện của tam giác ABC để tứ giác AMHN là hình vuông.Bài 2:Cho tam giác ABC cân tại A,có đường cao AH. Gọi M là trung điểm của AC, K là điểm đối xứng của H qua M.a)Chứng minh tứ giác AMHN là hình chữ nhật.b)Tứ giác ABHK là hình gì...
Đọc tiếp
Bài 1:
Cho tam giác ABC vuông tại A,đường cao AH.Gọi D là là điểm đối xứng với H qua AB M là giao điểm của AB và DH. Gọi E là đối xứng với H qua AC ,N là giao điểm của AC và HE.
a)Chứng minh tứ giác AMHN là hình chữ nhật
b)Chứng minh rằng D đối xứng với E qua A
c) Tìm điều kiện của tam giác ABC để tứ giác AMHN là hình vuông.
Bài 2:
Cho tam giác ABC cân tại A,có đường cao AH. Gọi M là trung điểm của AC, K là điểm đối xứng của H qua M.
a)Chứng minh tứ giác AMHN là hình chữ nhật.
b)Tứ giác ABHK là hình gì?Chứng minh.
c)Tìm điều kiện của tam giác ABC để là hình vuông.
Cho tam giác nhọn ABC (AB<AC),đường cao Ah.Gọi M là trung điểm của AB,D là điểm đối xứng với H qua M.
a)Chứng mính tứ giác AHBD là hình chữ nhật
b)Biết AB=10cm,BH= 6cm.Tính diện tích hình chữ nhật AHBD
c)Gọi I,N lần lượt là trung điểm của BC và AC.Chứng minh IHMN là hình thang cân
nhờ mọi người giảo hộ mình câu này với ạ
a: Xét tứ giác AHBD có
M là trung điểm chung của AB và HD
góc AHB=90 độ
=>AHBD là hình chữ nhật
b: \(AH=\sqrt{10^2-6^2}=8\left(cm\right)\)
\(S_{AHBD}=6\cdot8=48\left(cm^2\right)\)
c: Xét ΔABC có AM/AB=AI/AC
nênMI//BC
Xét ΔBAC có CN/CB=CI/CA
nên NI//AB và NI/AB=CN/CB=1/2
=>NI=HM
Xét tứ giác MINH có
MI//HN
MH=IN
Do đó: MINH là hình thang cân
Đúng 0
Bình luận (0)



















