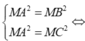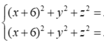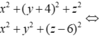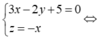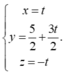Trong không gian Oxyz, cho các điểm A 2 ; − 2 ; 1 , B 1 ; − 1 ; 3 . Tọa độ của vectơ A B → là:
A. (1;-1;-2)
B. (-1;1;2)
C. (3;-3;4)
D. (-3; 3; -4)
Trong không gian Oxyz, cho các điểm A(-1;2;-3), B(2;-1;0). Tìm tọa độ véc-tơ ![]()
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho các điểm A ( 2 ; - 2 ; 1 ) , B ( 1 ; - 1 ; 3 ) . Tọa độ của vectơ A B → là
A. (1;-1;-2)
B. (-1;1;2)
C. (3;-3;4)
D. (-3;3;-4)
Trong không gian Oxyz, cho các điểm A(2;-2;1), B(1;-1;3). Tọa độ của véctơ A B → là
A. (1 ;-1 ;-2)
B. (-1 ;1 ;2)
C. (3 ;-3 ;4)
D. (-3 ;3 ;-4)
Trong không gian Oxyz, cho các điểm A(2;-2;1), B(1;-1;3). Tọa độ của vecto A B → là:
![]()
![]()
![]()
![]()
Đáp án A.
Phương pháp:
+) Cho hai điểm ![]()
Khi đó ta có: ![]()
Cách giải:
Ta có:
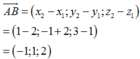
Trong không gian Oxyz, cho điểm A(2;-3;4). Lập phương trình mặt phẳng (P) đi qua các hình chiếu vuông góc của điểm A trên các trục tọa độ:
A. 2x-3y+4z-29=0
B. 2x-3y+4z-1=0
C. x 2 + y - 3 + z 4 = 0
D. x 2 + y - 3 + z 4 = 1
Đáp án D
Với điểm A(2;-3;4). Hình chiếu của A trên 3 trục tọa độ lần lượt là:
B(2; 0; 0); C( 0; -3; 0) và D( 0; 0; 4).
Phương trình mặt phẳng (BCD) là:
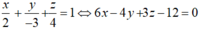
Trong không gian Oxyz, cho điểm A(2; –1;1). Phương trình mặt phẳng (α) đi qua hình chiếu của điểm A trên các trục tọa độ là
A. x 2 = y - 1 = z 1 = 0
B. x 2 + y - 1 + z 1 = 1
C. x 2 + y 1 + z 1 = 1
D. x 2 + y - 1 + z 1 = - 1
Đáp án B
Phương pháp:
Hình chiếu của điểm M(x0;y0;z0) trên trục Ox là điểm M1(x0;0;0)
Hình chiếu của điểm M(x0;y0;z0) trên trục Oy là điểm M2(0;y0;0)
Hình chiếu của điểm M(x0;y0;z0) trên trục Oz là điểm M3(0;0;z0)
Phương trình theo đoạn chắn của mặt phẳng đi qua 3 điểm
A(a;0;0), B(0;b;0), C(0;0;c), (a,b,c ≠ 0) là: x a + y b + z c = 1
Cách giải: Hình chiếu của điểm A(2; –1;1) trên các trục tọa độ Ox, Oy, Oz lần lượt là: (2;0;0), (0; –1;0), (0;0;1)
Phương trình mặt phẳng (α): x 2 + y - 1 + z 1 = 1
Trong không gian Oxyz, cho điểm A(2;-1;1). Phương trình mặt phẳng α đi qua hình chiếu của điểm A trên các trục tọa độ là
A. x 2 + y - 1 + z 1 = 0
B. x 2 + y - 1 + z 1 = 1
C. x 2 + y 1 + z 1 = 1
D. x 2 + y - 1 + z 1 = - 1
Đáp án B
Phương pháp:
Hình chiếu của điểm M ( x 0 ; y 0 ; z 0 ) trên trục Ox là điểm M 1 ( x 0 ; 0 ; 0 )
Hình chiếu của điểm M ( x 0 ; y 0 ; z 0 ) trên trục Oy là điểm M 2 ( 0 ; y 0 ; 0 )
Hình chiếu của điểm M ( x 0 ; y 0 ; z 0 ) trên trục Oz là điểm M 3 ( 0 ; 0 ; z 0 )
Phương trình theo đoạn chắn của mặt phẳng đi qua 3 điểm A(a;0;0), B(0;b;0), C(0;0;c) (a,b,c ≠ 0 ) là
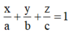
Cách giải: Hình chiếu của điểm A(2;-1;1) trên các trục tọa độ Ox, Oy, Oz lần lượt là: (2;0;0), (0;-1;0),(0;0;1).
Phương trình mặt phẳng α : x 2 + y - 1 + z 1 = 1
Trong không gian Oxyz, cho điểm M(2;-5;4). Trong các phát biểu sau, phát biểu nào sai?
A. Khoảng cách từ M đến mặt phẳng tọa độ (xOz) bằng 5
B. Khoảng cách từ M đến trục Oz bằng 29
C. Tọa độ điểm M’ đối xứng với M qua mặt phẳng (yOz) là M’(2;5;-4)
D.Tọa độ điểm M’ đối xứng với M qua trục Oy là M’(-2;-5;-4)
Trong không gian tọa độ Oxyz, cho A(2;0;0),B(0;2;0),C(0;0;2). Có tất cả bao nhiêu điểm M trong không gian thỏa mãn M không trùng với các điểm A, B, C và A M B ^ = B M C ^ = C M A ^ = 90 o
A. 0
B. 1
C. 2
D. 3
Trong không gian Oxyz, cho ba điểm A(-6;0;0), B(0;-4;0), C(0;0;6). Tập hợp tất cả các điểm M trong không gian cách đều ba điểm A, B, C là một đường thẳng có phương trình là
![]()
![]()

![]()
Chọn đáp án C.
Gọi M(x;y;z) ta có
hệ điều kiện