Cho hình chóp S.ABCDđáy là hình chữ nhật. Biết S A = A B = a , A D = 2 a , S A ⊥ A B C D . Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
A. 2 a 39 13
B. a 3 2
C. 3 a 3 4
D. a 6 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật cạnh a, S A ⊥ (A B C D) ,SC tạo với mặt đáy một góc 60 độ và (SAB ) một góc a với sin a = căn 3/ 4 . Tính chiều cao khối chóp.
Đáy là hình vuông hay chữ nhật bạn? Hình chữ nhật sao có các cạnh bằng nhau và bằng a được?
Cho hình chóp S. ABCD đáy là hình chữ nhật. Biết SA =AB = a, AD =2a, SA vuông góc (ABCD). Tính bán kính mặt cầu ngoại tiếp hình chóp S. ABCD.
A. 2 a 39 13
B. a 3 2
C. 3 a 3 4
D. a 6 2
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật, AB = a, AD = a 2 . Biết SA ⊥ ABCD và góc giữa đường thẳng SC với mặt phẳng đáy bằng 45 0 . Thể tích khối chóp S. ABCD bằng:
A . a 3 2
B . 3 a 3
C . a 3 6
D . a 3 6 3
Đáp án D
Dễ thấy ![]()
Lại có ∆SAC vuông tại A
=> AC = SA = ![]()
Vậy VS.ABCD = ![]()
cho hình chóp S ABCD có đáy ABCD là hình chữ nhật. Biết AB= a căn 2; AD= a căn 3; SA vuông góc (ABCD), biết SC = a căn 7
a, tính góc giữa SB và (ABCD)
b. tính góc giữa SC và (SAD)
c, tính góc giữa (SBC) và (ABCD)
d, tính góc giữa (SBD) và (ABCD)
a: (SB;(ABCD))=(BS;BA)=góc SBA
AC=căn a^2+3a^2=2a
SA=căn SC^2-AC^2=a*căn 3
tan SBA=SA/AB=căn 3
=>góc SBA=60 độ
b: (SC;(SAD))=(SC;SD)=góc SCD
SD=căn SA^2+AD^2=2a*căn 3
cos SCD=(CS^2+CD^2-SD^2)/(2*CS*CD)=-2/căn 7
=>góc SCD=139 độ
Cho hình chóp S.ABCD có đáy là hình chữ nhật, hình chiếu của S lên đáy trùng với trung điểm của AB. Tính thể tích V của hình chóp đã cho, biết rằng AB = a, BC = a 6 , khoảng cách từ A đến mặt (SCD) bằng 6 a/3
A. V = 6 6 a 3
B. V = 2 4 a 3
C. V = 2 2 a 3
D. V = 2 6 a 3
Đáp án C
Gọi M, N lần lượt là trung điểm của AB, CD, H là chân đường vuông góc kẻ từ M tới SN. Khi đó SM ⊥ (ABCD). Vì AB // CD nên AB // (ABCD), do đó d(A, (SCD)) = d(M, (SCD)) = MH
Ta có
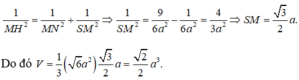
Cho hình chóp S. ABCD có đáy là hình chữ nhật, AB = a, AD = a 2 . Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của BC, SH = a 2 2 . Tính bán kính mặt cầu ngoại tiếp hình chóp S. BHD.
A. a 2 2
B. a 5 2
C. a 17 4
D. a 11 4
Chọn C
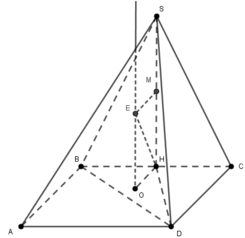
Gọi R và r lần lượt là bán kính mặt cầu ngoại tiếp hình chóp S. BHD và tam giác BHD.
Ta có HB= a 2 2 , H D = H C 2 + D C 2 = a 2 2 2 + a 2 = a 6 2 , B D = a 2 + 2 a 2 = a 3
Áp dụng định lí Cô sin, ta có
cos B H D ^ = a 2 2 + 3 a 2 2 - 3 a 2 2 . a 2 2 a 6 2 = - 1 3 ⇒ sin B H D ^ = 2 3
Diện tích tam giác BHD là
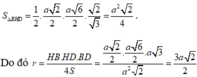
Gọi O là tâm đường tròn ngoại tiếp tam giác BHD và M là trung điểm SH. Mặt phẳng trung trực của SH cắt trục đường tròn ngoại tiếp tam giác BHD tại E. Khi đó E là tâm mặt cầu cần tìm.
Ta có
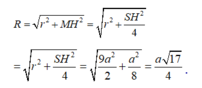
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O. AB=a,BD=a căn 3 biết hình chiếu của S lên (ABCD) là điểm M với M là trung điểm OB. Đồng thời SH= a căn3
a) Tính góc giữa (SCD) và (ABCD)
b) Khoảng cách (SD, BC)
c) Khoảng cách (SB,AC)
Chắc đề là \(SM=a\sqrt{3}\) vì không có điểm H nào trong dữ liệu
\(BC=AD=\sqrt{BD^2-AB^2}=a\sqrt{2}\)
a.
Qua M kẻ đường thẳng song song BC cắt CD tại E
\(\Rightarrow CD\perp ME\Rightarrow CD\perp\left(SME\right)\)
\(\Rightarrow\widehat{SEM}\) là góc giữa (SCD) và (ABCD)
Áp dụng định lý talet trong tam giác BCD:
\(\dfrac{EM}{BC}=\dfrac{DM}{BD}=\dfrac{3}{4}\Rightarrow EM=\dfrac{3}{4}BC=\dfrac{3a\sqrt{2}}{4}\)
\(\Rightarrow tan\widehat{SEM}=\dfrac{SM}{EM}=\dfrac{2\sqrt{6}}{3}\)
\(\Rightarrow\widehat{SEM}\approx58^031'\)
b.
\(BC||AD\Rightarrow BC||\left(SAD\right)\)
\(\Rightarrow d\left(BC;AD\right)=d\left(BC;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Lại có: BM cắt (SAD) tại D, mà \(BD=\dfrac{4}{3}MD\)
\(\Rightarrow d\left(B;\left(SAD\right)\right)=\dfrac{4}{3}d\left(M;\left(SAD\right)\right)\)
Trong mp (ABCD), từ M kẻ \(MH\perp AD\)
Trong mp (SMH), từ M kẻ \(MK\perp SH\)
\(\Rightarrow MK\perp\left(SAD\right)\Rightarrow MK=d\left(M;\left(SAD\right)\right)\)
Talet cho tam giác ABD:
\(\dfrac{MH}{AB}=\dfrac{MD}{BD}=\dfrac{3}{4}\Rightarrow MH=\dfrac{3}{4}AB=\dfrac{3a}{4}\)
Hệ thức lượng trong tam giác vuông SMH:
\(MK=\dfrac{SM.MH}{\sqrt{SM^2+MH^2}}=\dfrac{3a\sqrt{19}}{19}\)
\(\Rightarrow d\left(SD;BC\right)=\dfrac{4}{3}MK=\dfrac{4\sqrt{19}}{19}\)
c.
Qua B kẻ đường thẳng d song song AC
Trong mp (ABCD), từ M hạ \(MF\perp d\)
\(AC||d\Rightarrow AC||\left(SBF\right)\Rightarrow d\left(AC;SB\right)=d\left(AC;\left(SBF\right)\right)=d\left(O;\left(SBF\right)\right)\)
Mà \(OM\) cắt \(\left(SBF\right)\) tại B đồng thời \(OB=2MB\)
\(\Rightarrow d\left(O;\left(SBF\right)\right)=2d\left(M;\left(SBF\right)\right)\)
Trong mp (SMF), từ M hạ \(MI\perp SF\)
\(\Rightarrow MI\perp\left(SBF\right)\Rightarrow MI=d\left(M;\left(SBF\right)\right)\)
Ta có: \(\widehat{MBF}=\widehat{AOB}\) (so le trong)
\(cos\widehat{AOB}=\dfrac{OA^2+OB^2-AB^2}{2OA.OB}=\dfrac{1}{3}\)
\(\Rightarrow cos\widehat{MBF}=\dfrac{1}{3}\Rightarrow MF=BM.cos\widehat{MBF}=\dfrac{1}{4}BD.\dfrac{1}{3}=\dfrac{a\sqrt{3}}{12}\)
Áp dụng hệ thức lượng trong tam giác vuông SMF:
\(MI=\dfrac{SM.MF}{\sqrt{SM^2+MF^2}}=...\)
\(\Rightarrow d\left(SB;AC\right)=2MI=...\)
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Biết A(0;0;0), D(2;0;0), B(0; 4;0).
A. 2
B. 1 2
C. 2 2
D. 2
Cho hình chóp S.ABCD, đáy là hình chữ nhật, S A ⊥ A B C D . Biết AB=a AD=2a, góc giữa SC và (SAB) là 60 ° . Khi đó d(B;(SDC)) là
A. 2 a 15 .
B. 2 a 7 .
C. 2 a 11 11 .
D. 22 a 15 .