Cho a, b là các số thực dương thỏa mãn a ≠ 1 , a ≠ 1 b và log a b = 5 . Tính P = log a b b a .
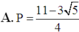
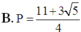
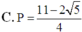
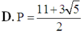
Các Ctv hoặc các giáo viên helpp ạ
Cho a,b,c là số thực dương không âm thỏa mãn
Cho a,b,c là số thực dương không âm thỏa mãn \(a+b+c=1\) . Chứng minh rằng :
\(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}>10\)
cho a,b là là các số thực dương thỏa mãn: a+b=1.chứng minh: (a+\(\dfrac{1}{a}\))(b+\(\dfrac{1}{b}\)) ≥ \(\dfrac{25}{4}\)
Áp dụng BĐT cosi:
\(\left(a+\dfrac{1}{a}\right)\left(b+\dfrac{1}{b}\right)4=ab+\dfrac{a}{b}+\dfrac{b}{a}+\dfrac{1}{ab}\\ \ge ab+\dfrac{1}{ab}+2\sqrt{\dfrac{a}{b}\cdot\dfrac{b}{a}}=ab+\dfrac{1}{ab}+2\)
Áp dụng tiếp BĐT cosi:
\(ab+\dfrac{1}{ab}=\left(16ab+\dfrac{1}{ab}\right)-15ab\\ \ge2\sqrt{\dfrac{16ab}{ab}}-15ab=8-15ab\\ \ge8-15\cdot\dfrac{a+b}{4}=8-15\cdot\dfrac{1}{4}=\dfrac{17}{4}\)
\(\Leftrightarrow ab+\dfrac{a}{b}+\dfrac{b}{a}+\dfrac{1}{ab}\ge\dfrac{17}{4}+2=\dfrac{25}{4}\)
Dấu \("="\Leftrightarrow a=b=\dfrac{1}{2}\)
Cho a, b là các số thực dương thỏa mãn a ≠ 1 , a ≠ b và log a b = 2 . Tính P = log b a a b .
A. P = 1 - 2 2 2 - 1
B. P = 1 + 2 2 2 + 1
C. P = 1 - 2 2 2 + 1
D. P = 1 + 2 2 2 - 1
Đáp án A
Ta có P = 1 2 . 1 - log a b log a b - 1 2 = 1 - 2 2 2 - 1 .
Cho a, b là các số thực dương thỏa mãn a ≠ 1 , a ≠ b và log a b = 2 . Tính P = log b a a b
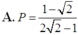
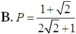
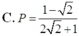
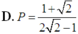
cho a,b là các số thực dương thỏa mãn a+b =<1.Tìm gtnn của A=1/(a^2+b^2)+1/2ab
Ta có : (a-b)^2 >= 0 với mọi a,b
<=> a^2-2ab+b^2 >= 0
<=> a^2+b^2 >= 2ab
<=> a^2+2ab+b^2 >= 4ab
<=> (a+b)^2 >= 4ab
Với a,b > 0 thì ta chia 2 vế cho ab .(+b) được :
a+b/ab >= 4/a+b
<=>1/a + 1/b >=4ab
Áp dụng bđt trên thì A >= 4/(a^2+b^2+2ab) = 4/(a+b)^2 >= 4/1^2 = 4
Dấu "=" xảy ra <=> a=b ; a+b =1 <=> a=b=1/2
Vậy Min A = 4 <=> x = y= 1/2
`a+ble1<=>(a+b)^2le1`
Áp dụng bđt `1/(a)+1/bge4/(a+b)` ta có:
`Age4/(a^2+2ab+b^2)=4/(a+b)^2=4/1=4`
Dấu `=` xảy ra khi:`a^2+b^2=2ab<=>(a-b)^2=0<=>a=b` và `a+b=1`
`<=>a=b=1/2`
Vậy GTNN của `A=4` khi và chỉ khi `a=b=1/2`
Cho a,b là các số thực dương thỏa mãn ab=1. Tìm GTNN của:
\(P=\dfrac{a^2}{1+b}+\dfrac{b^2}{1+a}\)
cho a,b là các số thực dương thỏa mãn ab>=1
chứng minh: 1/(1+a^2)+1/(1+b^2)>=2(1+ab)
\(\dfrac{1}{1+a^2}+\dfrac{1}{1+b^2}=\dfrac{a^2+b^2+2}{a^2b^2+a^2+b^2+1}=1-\dfrac{a^2b^2-1}{a^2b^2+a^2+b^2+1}\ge1-\dfrac{a^2b^2-1}{a^2b^2+2ab+1}=\dfrac{2}{ab+1}\)
Dấu "=" xảy ra khi \(a=b\) hoặc \(ab=1\)
\(< =>VT< =>\dfrac{a^2+b^2+2}{\left(1+a^2\right)\left(1+b^2\right)}=\dfrac{a^2+b^2+2}{a^2+a^2b^2+b^2+1}\)
\(VT\ge VP\)(giả thiết)
\(< =>\dfrac{a^2+b^2+2}{a^2+a^2b^2+b^2+1}\ge\dfrac{2}{1+ab}\)
\(< =>a^2+b^2+2+a^3b+ab^3+2ab-2a^2-2b^2-2a^2b^2-2\ge0\)
\(< =>\left(a-b^{ }\right)^2\left(ab-1\right)\ge0\)(luôn đúng với mọi a,b là các số thực dương thỏa mãn \(ab\ge1\))
\(\)
Cho a,b là các số thực dương a>1,a#b và thỏa mãn log a b = 2 . Khi đó log a b a b bằng
A. - 3 2
B. -6
C. 3 2
D. 0
Đổi về cơ số a có
log a b a b = log a a b log a a b = 1 2 1 + log a b 1 - log a b = 1 2 ( 1 + 2 ) 1 - 2 = - 3 2
Chọn đáp án A.
Cho a,b là các số thực dương thỏa mãn a+b=1.Chứng minh rnằng a^2/a+1+b^2/b+1=>1/3
Áp dụng BĐT Cauchy-Schwarz dạng Engel,ta có:
\(A=\frac{a^2}{a+1}+\frac{b^2}{b+1}\ge\frac{\left(a+b\right)^2}{a+b+2}=\frac{1}{1+2}=\frac{1}{3}^{\left(đpcm\right)}\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}a+b=1\\\frac{a}{a+1}=\frac{b}{b+1}\end{cases}}\Leftrightarrow\hept{\begin{cases}a+b=1\\ab+a=ab+b\end{cases}}\Leftrightarrow a=b=\frac{1}{2}\)
Vậy ...
Cho a, b là các số thực dương thỏa mãn a ≠ 1 , a ≠ 1 b và log a b = 5 . Tính P = log a b b a .
A. P = 11 − 3 5 4
B. P = 11 + 3 5 4
C. P = 11 − 2 5 4
D. P = 11 + 3 5 2
Đáp án A
Ta có: P = log a b b a = 2 log a b b a
= 2 log a b b − log a b a = 2 1 log b a b − 1 2 log a b a
= 2 1 1 + log b a − 1 2 . 1 log a a b = 2 1 1 + 1 log a b − 1 2 . 1 1 + log a b = 2 1 1 + 1 5 − 1 2 . 1 1 + 5 = 11 − 3 5 4