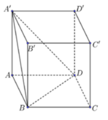
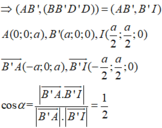Cho hình lập phương ABCD. A'B'C'D' cạnh bằng a. Góc giữa B'D và mặt phẳng (AA'D'D) gần nhất với góc nào sau đây?
A. 20 o
B. 35 o
C. 45 o
D. 60 o
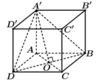
Cho hình lập phương ABCD.A'B'C'D' cạnh a
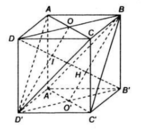
a) Chứng minh rằng B'D vuông góc với mặt phẳng (BA'C')
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD')
c) Tính khoảng cách giữa hai đường thẳng BC' và CD'
Cho hình lập phương ABCD.A'B'C'D'
a) Chứng minh rằng B'D vuông góc với mặt phẳng (BA'C')
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD')
c) Tính khoảng cách giữa hai đường thẳng BC' và CD'
b) Xét tứ giác A’BCD’ có BC//A’D’ và BC = A’D’
=> tứ giác A’BCD’ là hình bình hành
=> BA’ // CD’ ( tính chất của hình bình hành)
Tương tự, tứ giác ABC’D’ là hình bình hành nên BC’//AD’
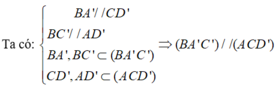
Gọi O và O’ là tâm của ABCD và A’B’C’D’.
Gọi H và I lần lượt là tâm của hai tam giác đều BA’C’ và ACD’.
* Xét ( BB’D’D) có BO’// D’O nên OI // HB
Lại có: O là trung điểm BD
=> I là trung điểm của HD: IH = ID (1)
* Xét (BB’D’D) có D’O// BO’ nên D’I // HO’
Lại có: O’ là trung điểm của B’D’ nên H là trung điểm B’I: HI = HB’ (2)
Từ (1) và (2) suy ra: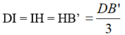 
* Theo phần trên B'D ⊥ (BA'C) ⇒ IH ⊥ (BA'C)
Mà I ∈ (ACD') nên khoảng cách giữa hai mp song song (ACD’) và ( BA’C’) là độ dài đoạn IH.
Khi đó:
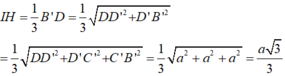
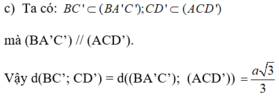
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a . Tính góc giữa 2 đường thẳng A'B và B'D'
\(BD||B'D'\Rightarrow\widehat{\left(A'B;B'D'\right)}=\widehat{\left(A'B;BD\right)}=\widehat{A'BD}\)
Mặt khác \(A'B=BD=A'D=a\sqrt{2}\) (đều là đường chéo của các hình vuông cạnh a)
\(\Rightarrow\Delta A'BD\) đều \(\Rightarrow\widehat{A'BD}=60^0\)
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Sin của góc tạo bởi giữa hai mặt phẳng (BDA') và (ABCD) bằng
A. 3 3
B. 6 3
C. 3 4
D. 6 4
Gọi 
Ta chứng minh được 
Từ (1) và (2) suy ra 
Vậy 
Chọn B
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Số đo của góc giữa hai mặt phẳng (BA’C) và (DA’C) là
A. 90 0
B. 60 0
C. 30 0
D. 45 0
Cho hình lập phương \(ABCD.A'B'C'D'\). Tính góc giữa các đường thẳng sau đây với mặt phẳng \(\left( {ABCD} \right)\):
a) \(AA'\);
b) \(BC'\);
c) \(A'C\).
THAM KHẢO:
a) Vì AA′⊥(ABCD) nên góc giữa đường thẳng AA' và (ABCD) là \(90^0\)
b) CC′⊥(ABCD) nên C là hình chiếu vuông góc của C' lên (ABCD).
Suy ra góc giữa BC' và (ABCD) là \(\widehat{C'BC}\)=\(45^O\) (Vì BCC'C' là hình vuông)c) Gọi cạnh của hình lập phương là a
Ta có: AC=\(a\sqrt{2}\),tan \(\widehat{ACA'}\)=\(\dfrac{1}{\sqrt{2}}\) nên \(\widehat{ACA'}\)=\(35^O\)
AA′⊥(ABCD) nên A là hình chiếu vuông góc của A' lên (ABCD)
Suy ra góc giữa A'C và (ABCD) là \(\widehat{ACA'}\)=\(35^O\)
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a (tham khảo hình vẽ). Giá trị s i n của góc giữa hai mặt phẳng B D A ' và A B C D bằng
A. 6 4 .
B. 3 3 .
C. 6 3 .
D. 3 4 .
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a, gọi α là góc giữa đường thẳng AB' và mặt phẳng (BB'D'D). Tính sin α .
A. 3 4 .
B. 3 2 .
C. 3 5 .
D. 1 2 .
Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ ( B B ' D ' D ) ⇒ B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)
