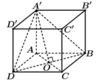
Gọi ![]()
Ta chứng minh được ![]()
Từ (1) và (2) suy ra ![]()
Vậy ![]()
Chọn B

Gọi ![]()
Ta chứng minh được ![]()
Từ (1) và (2) suy ra ![]()
Vậy ![]()
Chọn B
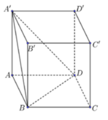
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a (tham khảo hình vẽ). Giá trị s i n của góc giữa hai mặt phẳng B D A ' và A B C D bằng
A. 6 4 .
B. 3 3 .
C. 6 3 .
D. 3 4 .
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng 3 Mặt phẳng α cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi mặt phẳng α biết α tạo với mặt A B B ' A ' một góc 60 °
A. 2 3
B. 3 2
C. 6
D. 3 3 2
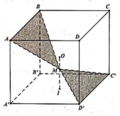
Cho hình lập phương ABCD.A'B'C'D' tâm O. Gọi I là tâm của hình vuông A'B'C'D' và điểm M thuộc đoạn OI sao cho M O = 1 2 M I (tham khảo hình vẽ). Khi đó sin góc tạo bởi hai mặt phẳng (MC'D') và (MAB) bằng:
A. 6 13 65
B. 7 85 85
C. 7 13 65
D. 6 85 85
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng 1. Khoảng cách từ điểm A đến mặt phẳng (BDA') bằng
A. 3
B. 2 2
C. 3 3
D. 6 4
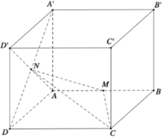
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ các đỉnh A(0;0;0),B(1;0;0), D(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADD'A'. Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng
A. 3 5 4 14
B. 14 4
C. 3 14 4 5
D. 9 4 14
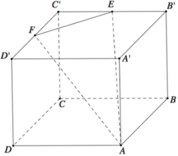
Cho hình lập phương ABCD.A'B'C'D'. Gọi E, F lần lượt là trung điểm các cạnh B'C', C'D'. Côsin góc giữa hai mặt phẳng (AEF) và (ABCD) bằng
A. 3 17 17
B. 2 34 17
C. 4 17 17
D. 17 17
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a, gọi α là góc giữa đường thẳng AB' và mặt phẳng (BB'D'D). Tính sin α .
A. 3 4 .
B. 3 2 .
C. 3 5 .
D. 1 2 .
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a, gọi α là góc giữa đường thẳng A ' B và mặt phẳng B B ' D ' D . Tính sin α .
A. 3 5 .
B. 3 2 .
C. 1 2 .
D. 3 4 .
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Góc giữa B'D và mặt phẳng (AA'D'D) gần nhất với góc nào sau đây?
A. 20 °
B. 35 °
C. 45 °
D. 60 °