Cho tam giác ABC. D là điểm nằm giữa B và C. CMR AD < chu vi tam giác ABC

Những câu hỏi liên quan
cho tam giác ABC, điểm D nằm giữa B và C. CMR: AD < nửa chu vi tam giác ABC
Bài 4: Cho tam giác ABC,điểm D là điểm nằm giữa B và C.
a) Chứng minh AD bé hơn nửa chu vi tam giác ABC
b) E là điểm nằm tùy ý ở bên trong tam giác ABC chứng minh tổng khoảng cách từ E đến mỗi đỉnh của tam giác luôn lớn hơn nửa chu vi và bé hơn chu vi tam giác ABC.
cho tam giác ABC : điểm D nằm giữa B và C . CM : AD < nửa chu vi tam giác ABC
....Có ở trong sách bài tập toán 7 (tập II) mà bn......:))
Đúng 0
Bình luận (1)
Xét \(\Delta\) ADB có :
AD < AB + BD ( Bất đẳng thức tam giác )
Xét \(\Delta\)ADC có :
AD < AC + CD ( Bất đẳng thức tam giác )
Cộng hai vế của đẳng thức lại với nhau,ta có :
2AD < AB + BD + AC + CD
=> 2AD < AB + AC +(BD + CD)
=> 2AD < AB + AC + BC
hay AD < \(\dfrac{AB+AC+BC}{2}\)(nửa chu vi tam giác ABC) ( đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.
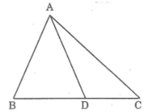
Trong ΔABD, ta có:
AD < AB + BD (bất đẳng thức tam giác) (1)
Trong ΔADC, ta có:
AD < AC + DC (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2), ta có:
2AD < AB + BD + AC + DC ⇔ 2AD < AB + AC + BC
Vậy AD < (AB + AC + BC) / 2 .
Đúng 1
Bình luận (0)
Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.
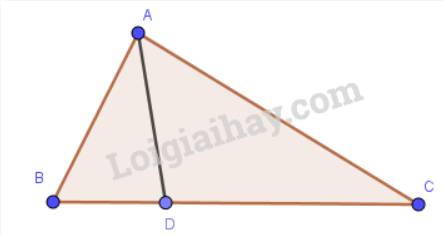
Áp dụng quan hệ giữa ba cạnh của tam giác ABD, ta có: AD < AB + BD
Áp dụng quan hệ giữa ba cạnh của tam giác ACD, ta có: AD < CD + AC
\(\Rightarrow AD + AD < AB+BD+CD+AC\)
\(\Rightarrow 2AD<AB+BC+AC\) ( vì \(DB+DC=BC\))
\(\Rightarrow\) 2AD < Chu vi tam giác ABC hay AD < (Chu vi tam giác ABC) : 2
Vậy AD nhỏ hơn nửa chu vi tam giác ABC.
Đúng 0
Bình luận (0)
cho tam giác ABC, điểm D nằm giữa B và C. chứng minh AD nhỏ hơn nữa chu vi tam giác ABC
Trong ΔABD, ta có:
AD < AB + BD (bất đẳng thức tam giác) (1)
Trong ΔADC, ta có:
AD < AC + DC (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2), ta có:
2AD < AB + BD + AC + DC ⇔ 2AD < AB + AC + BC
Vậy AD < (AB + AC + BC) / 2 .
Đúng 0
Bình luận (0)
Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC ?
XétΔABD có AD<AB+BD(1)
Xét ΔACD có AD<AC+CD(2)
Từ (1) và (2) suy ra \(2AD< AB+AC+BC\)
hay \(AD< \dfrac{AB+AC+BC}{2}=\dfrac{C_{ABC}}{2}\)
Đúng 1
Bình luận (0)
Bài 1 : cho tam giác ABC, M là điểm nằm trong tam giác. CM MB+MC<AB+AC
Bài 2: cho tam giác ABC, điểm nằm giữa B và D. CMR: AD < nửa chu vi tam giác ABC
P/s: GIÚP VỚI!!!! Mk cần bài này trước 15h chiều ngày mai và vẽ hình+ làm từng bước ra hộ mk nhé. Love <3
Cho tam giác ABC vẽ AH vuông góc BC. D,E,F lần lượt là các điểm nằm trong A và H nằm giữa B và H nằm giữa Cvà H
Chu vi tam giác BEF < tam giác ABC với vị trí nào điểm D,E,F thì chu vi tam giác DEF = 1/2 chu vi tam giác ABC



















