Cho tích phân ∫ 1 2 ln x x 2 d x = b c + a ln 2 với a là số thực, b và c là các số nguyên dương, đồng thời b c là phân số tối giản. Tính giá trị của biểu thức P=2a+3b+c
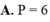

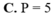
![]()
Tính các tích phân sau: 1) 2 ln e e x dx ; 2) 1 3 2 0 4 x dx x ; 3) /2 /4 1 tan dx x ; 4) 1 0 x e dx ; 5) 2 1 x xe dx ; 6) 0 1 3 4 dx x ; 7) 2 1 4 4 5 dx x x ; 8) 2 0 ln 1 x dx x (HD: 1 u x ) ĐS: 1) 2 e ; 2) 16 7 5 3 ; 3) ln 2 ; 4) 2
Áp dụng phương pháp tính tích phân, hãy tính các tích phân sau :
a) \(\int\limits^{\dfrac{\pi}{2}}_0x\cos2xdx\)
b) \(\int\limits^{\ln2}_0xe^{-2x}dx\)
c) \(\int\limits^1_0\ln\left(2x+1\right)dx\)
d) \(\int\limits^3_2\left|\ln\left(x-1\right)-\ln\left(x+1\right)\right|dx\)
e) \(\int\limits^2_{\dfrac{1}{2}}\left(1+x-\dfrac{1}{x}\right)e^{x+\dfrac{1}{x}}dx\)
g) \(\int\limits^{\dfrac{\pi}{2}}_0x\cos x\sin^2xdx\)
h) \(\int\limits^1_0\dfrac{xe^x}{\left(1+x\right)^2}dx\)
i) \(\int\limits^e_1\dfrac{1+x\ln x}{x}e^xdx\)
Cho tích phân I = ∫ 0 1 ( x + 2 ) ln ( x + 1 ) d x = a l n 2 − 7 b trong đó a, b là các số nguyên dương. Tổng a + b 2 bằng
A. 8
B. 16
C. 12
D. 20
Tính tích phân của hàm số chứa Ln:
\(I=\int_{\varepsilon}^{\varepsilon^2}\left(\frac{1}{\ln^2x}-\frac{1}{\ln x}\right)dx\)
MỌI NGƯỜI GIÚP MÌNH CÂU TÍCH PHÂN NÀY VỚI!!!!!!!!
đặt t = lnx
tôi ko biết \(\varepsilon\) trong bài là gì, tuy nhiên nếu nó là số bất kì thì xét 2 TH sau để biết đk t
TH1: \(\varepsilon\in\left(0;1\right)\)
TH2: \(\varepsilon>1\)
Cho hàm số f(x) liên tục trên ℝ thỏa mãn ∫ 0 99 f ( x ) d x = 2 . Khi đó tích phân I = ∫ 0 e 99 - 1 x x 2 + 1 f ( ln ( x 2 + 1 ) ) d x bằng bao nhiêu?
A. 1.
B. 2.
C. 3.
D. 4.
Tính tích phân :
\(I=\int\limits^e_1\frac{\ln^2x}{x\left(1+2\ln x\right)}dx\)
\(I=\frac{1}{4}\int\limits^e_1\frac{4\ln^2x-1+1}{x\left(1+2\ln x\right)}dx=\frac{1}{4}\int\limits^e_1\frac{\left(2\ln x-1\right)dx}{x}+\frac{1}{4}\int\limits^e_1\frac{dx}{x\cdot\left(1+2\ln x\right)}\)
\(=\frac{1}{8}\int\limits^e_1\left(2\ln x-1\right)d\left(2\ln x-1\right)+\frac{1}{8}\int\limits^e_1\frac{d\left(2\ln x+1\right)}{\left(1+2\ln x\right)}\)
\(=\left(\frac{1}{16}\left(2\ln x-1\right)^2\right)|^e_1+\frac{1}{8}\ln\left|\left(1+2\ln x\right)\right||^e_1\)
\(=\frac{1}{8}\ln3\)
Tính tích phân sau :
\(\int\limits^2_1\frac{\ln\left(x+1\right)}{x^2}\)
\(\int\limits^2_1\frac{\ln\left(x+1\right)}{x^2}dx=-\frac{\ln\left(x+1\right)}{x^2}+\int\limits^2_1\frac{1}{x\left(x+1\right)}dx=\ln2-\frac{\ln3}{2}+\int\limits^2_1\left(\frac{1}{x}-\frac{1}{x+1}\right)dx\)
\(=\ln2-\frac{\ln3}{2}+\ln\left(\frac{x}{x+1}\right)|^2_1=\ln2-\frac{\ln3}{2}-\ln3=\frac{\ln2-3\ln3}{2}\)
4. Tính đạo hàm của các hàm số sau:
a) \(y = (3x^2-4x+1)^{-4}\)
b) \(y = 3^{x^2-1} + e^{-x+1}\)
c) \(y = \ln (x^2-4x) + \log_{3} (2x-1)\)
d) \(y =x . \ln x + 2^{\frac{x-1}{x+1}}\)
e) \(y = x^{-7} - \ln (x^2-1)\)
`a)TXĐ:R\\{1;1/3}`
`y'=[-4(6x-4)]/[(3x^2-4x+1)^5]`
`b)TXĐ:R`
`y'=2x. 3^[x^2-1] ln 3-e^[-x+1]`
`c)TXĐ: (4;+oo)`
`y'=[2x-4]/[x^2-4x]+2/[(2x-1).ln 3]`
`d)TXĐ:(0;+oo)`
`y'=ln x+2/[(x+1)^2].2^[[x-1]/[x+1]].ln 2`
`e)TXĐ:(-oo;-1)uu(1;+oo)`
`y'=-7x^[-8]-[2x]/[x^2-1]`
Lời giải:
a.
$y'=-4(3x^2-4x+1)^{-5}(3x^2-4x+1)'$
$=-4(3x^2-4x+1)^{-5}(6x-4)$
$=-8(3x-2)(3x^2-4x+1)^{-5}$
b.
$y'=(3^{x^2-1})'+(e^{-x+1})'$
$=(x^2-1)'3^{x^2-1}\ln 3 + (-x+1)'e^{-x+1}$
$=2x.3^{x^2-1}.\ln 3 -e^{-x+1}$
c.
$y'=\frac{(x^2-4x)'}{x^2-4x}+\frac{(2x-1)'}{(2x-1)\ln 3}$
$=\frac{2x-4}{x^2-4x}+\frac{2}{(2x-1)\ln 3}$
d.
\(y'=(x\ln x)'+(2^{\frac{x-1}{x+1}})'=x(\ln x)'+x'\ln x+(\frac{x-1}{x+1})'.2^{\frac{x-1}{x+1}}\ln 2\)
\(=x.\frac{1}{x}+\ln x+\frac{2}{(x+1)^2}.2^{\frac{x-1}{x+1}}\ln 2\\ =1+\ln x+\frac{2^{\frac{2x}{x+1}}\ln 2}{(x+1)^2}\)
e.
\(y'=-7x^{-8}-\frac{(x^2-1)'}{x^2-1}=-7x^{-8}-\frac{2x}{x^2-1}\)
Tính tích phân :
\(\int\limits^3_1\frac{3+\ln x}{\left(x+1\right)^2}dx\)
Khảo sát sự hội tụ phân kỳ của tích phân suy rộng
\(\int\limits^{\infty}_0\dfrac{\ln\left(\sqrt[3]{1+\dfrac{3}{4}x^{200}}\right)}{x^2}dx\)