Đặt log 2 3 = a , log 3 4 = b . Biểu diễn T = log 27 8 + log 256 81 theo a và b ta được T = x a 2 + y b 2 + 4 z a 2 b + a b 2 với x, y, z là các số thực. Hãy tính tổng 4 x 2 + y - z 3 .
A. 3
B. 4
C. 6
D. 2
Những câu hỏi liên quan
log(2)3=a , log(5)3 biểu diễn log(6)45 theo a,b
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 18:15
Đặt \(\log 2 = a,\log 3 = b\). Biểu thị các biểu thức sau theo \(a\) và \(b\).
a) \({\log _4}9\);
b) \({\log _6}12\);
c) \({\log _5}6\).
a: \(log_49=\dfrac{log9}{log4}=\dfrac{log3^2}{log2^2}=\dfrac{2\cdot log3}{2\cdot log2}=\dfrac{log3}{log2}=\dfrac{b}{a}\)
b: \(log_612=\dfrac{log12}{log6}=\dfrac{log2^2+log3}{log2+log3}=\dfrac{2\cdot log2+log3}{log2+log3}\)
\(=\dfrac{2a+b}{a+b}\)
c: \(log_56=\dfrac{log6}{log5}=\dfrac{log\left(2\cdot3\right)}{log\left(\dfrac{10}{2}\right)}=\dfrac{log2+log3}{log10-log2}\)
\(=\dfrac{a+b}{1-a}\)
Đúng 1
Bình luận (0)
Cho
log
2
a
,
log
3
b
. Biểu diễn
log
625
270
theo a và b là: A.
1
4
3
b
+
1
1
-
a
B....
Đọc tiếp
Cho log 2 = a , log 3 = b . Biểu diễn log 625 270 theo a và b là:
A. 1 4 3 b + 1 1 - a
B. a + 2 b 2 3 a 1 - b
C. a + b 2 4 a 1 - b
D. a + b 2 2 a 1 - b
Đặt log 3 p và log 5 q Hãy biểu diễn log1530 theo p và q A. B. C. D.
Đọc tiếp
Đặt log 3= p và log 5= q Hãy biểu diễn log1530 theo p và q
A.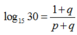 
B.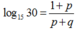 
C.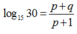 
D.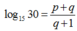 
Đặt m log 2 và n log 7. Hãy biểu diễn
log
6125
7
theo m và n.
Đọc tiếp
Đặt m = log 2 và n = log 7. Hãy biểu diễn log 6125 7 theo m và n.
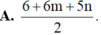
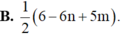
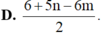
Đáp án D.
Ta có
log 6125 7 = log 6125 + log 7 = log 7 2 . 125 + 1 2 log 7
= 5 2 log 7 + log 5 3 = 5 2 n + 3 log 5 = 5 2 n + 3 1 - log 2
= 5 2 n + 3 - 3 m .
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
15 tháng 8 2023 lúc 19:13
Tính giá trị của các biểu thức sau:
a) \(A = {\log _2}3.{\log _3}4.{\log _4}5.{\log _5}6.{\log _6}7.{\log _7}8;\)
b) \(B = {\log _2}2.{\log _2}4...{\log _2}{2^n}.\)
\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 18:12
Đặt \({\log _3}2 = a,{\log _3}7 = b\). Biểu thị \({\log _{12}}21\) theo \(a\) và \(b\).
\(log_{12}21=\dfrac{log_321}{log_312}=\dfrac{log_3\left(7\cdot3\right)}{log_3\left(2^2\cdot3\right)}=\dfrac{log_37+log_33}{log_34+log_33}\)
\(=\dfrac{log_37+1}{log_32^2+1}=\dfrac{log_37+1}{2\cdot log_32+1}=\dfrac{b+1}{2a+1}\)
Đúng 0
Bình luận (0)
tính giá trị của biểu thức A=log32.log43.log54...log1615 là:
A.1 B.\(\dfrac{3}{4}\) C.\(\dfrac{1}{4} \) D.\(\dfrac{1}{2}\)
Lời giải:
Sử dụng công thức \(\log_ab=\frac{\ln b}{\ln a}\)
\(\Rightarrow A=\frac{\ln 2}{\ln 3}.\frac{\ln 3}{\ln 4}.\frac{\ln 4}{\ln 5}....\frac{\ln 15}{\ln 16}\)
\(\Leftrightarrow A=\frac{\ln 2}{\ln 16}=\log_{16}2=\frac{1}{4}\)
Đáp án C.
Đúng 0
Bình luận (0)
Đặt
a
log
2
5
,
b
log
3
5
. Hãy biểu diễn log 6 5 theo a và b. A.
log
6
5
1
a
+
b
B.
log
6
5
a...
Đọc tiếp
Đặt a = log 2 5 , b = log 3 5 . Hãy biểu diễn log 6 5 theo a và b.
A. log 6 5 = 1 a + b
B. log 6 5 = a b a + b
C. log 6 5 = a 2 + b 2
D. log 6 5 = a + b
1. cho a=log3 2 và b=log3 5. tính các logarit sau theo a, b; A=log3 80, B=log3 37,5
2. cho log10 3=a, log5=b. tính C=log30 8 theo a, b
3. cho log27 5=a, log8 7=b, log2 3=c. tính D log6 35 theo a, b, c
Bài 1:
\(A=\log_380=\log_3(2^4.5)=\log_3(2^4)+\log_3(5)\)
\(=4\log_32+\log_35=4a+b\)
\(B=\log_3(37,5)=\log_3(2^{-1}.75)=\log_3(2^{-1}.3.5^2)\)
\(=\log_3(2^{-1})+\log_33+\log_3(5^2)=-\log_32+1+2\log_35\)
\(=-a+1+2b\)
Đúng 0
Bình luận (0)
Bài 2:
\(\log_{30}8=\frac{\log 8}{\log 30}=\frac{\log (2^3)}{\log (10.3)}=\frac{3\log2}{\log 10+\log 3}\)
\(=\frac{3\log (\frac{10}{5})}{1+\log 3}=\frac{3(\log 10-\log 5)}{1+\log 3}=\frac{3(1-b)}{1+a}\)
Đúng 0
Bình luận (0)
Bài 3:
\(\log_{27}5=a; \log_87=b; \log_23=c\)
\(\Leftrightarrow \frac{\ln 5}{\ln 27}=a; \frac{\ln 7}{\ln 8}=b; \frac{\ln 3}{\ln 2}=c\)
\(\Leftrightarrow \frac{\ln 5}{\ln (3^3)}=a; \frac{\ln 7}{\ln (2^3)}=b; \ln 3=c\ln 2\)
\(\Leftrightarrow \frac{\ln 5}{3\ln 3}=a; \frac{\ln 7}{3\ln 2}=b; \ln 3=c\ln 2\)
\(\Rightarrow \frac{\ln 5}{3c\ln 2}=a; \frac{\ln 7}{3\ln 2}=b\)
\(\Rightarrow \ln 35=\ln 5+\ln 7=3ac\ln 2+3b\ln 2\)
Do đó:
\(D=\log_6 35=\frac{\ln 35}{\ln 6}=\frac{\ln 35}{\ln 2+\ln 3}=\frac{\ln 35}{\ln 2+c\ln 2}=\frac{3ac\ln 2+3b\ln 2}{\ln 2+c\ln 2}\)
\(=\frac{3ac+3b}{1+c}\)
Đúng 0
Bình luận (0)