Tổng các nghiệm của phương trình s i n 2 2 x s i n 2 4...

Hãy tham gia nhóm Học sinh Hoc24OLM

Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài

Chọn lớp:

Chọn môn:

Gửi câu hỏi ẩn danh

Pham Trong Bach 28 tháng 4 2017 lúc 3:56

Tổng các nghiệm của phương trình s i n 2 2 x + s i n 2 4 x 3 2 trên đoạn [0, π 2 ] là: A. 7 π 4 B. 3 π 4 C. ...

Đọc tiếp

Tổng các nghiệm của phương trình s i n 2 2 x + s i n 2 4 x = 3 2 trên đoạn [0, π 2 ] là:

A. 7 π 4

B. 3 π 4

C. π

D. 5 π 4

Lớp 0 Toán

Những câu hỏi liên quan

Uzumaki

15 tháng 5 2022 lúc 6:24

$\text{Chứng minh phương trình sau luôn có nghiệm: a c o s 2 x + b s i n x + c o s x = 0}$

Xem chi tiết

Lớp 11 Toán Chương 3: VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓ...

Sinphuya Kimito

15 tháng 5 2022 lúc 6:25

$\text{Đặt f (x)= a.cos2x+b.sinx+cosx}$

$\text{Hàm f (x) xác định và liên tục trên R}$

$\text{f ( π /4 ) = b √2 /2 + √2 /2 }$

$\text{f ( 5/π4 ) = − b √ 2/ 2 − √ 2/ 2 }$

$\text{⇒ f (π /4) . f ( 5 π/ 4 ) = − 1/2 ( b + 1 )^ 2 ≤ 0 ; ∀ a ; b ; c}$

$⇒ f (x)= 0 luôn có ít nhất 1 nghiệm thuộc đoạn [ π /4 ; 5π/4]$

Hay pt đã có nghiệm.

Đúng 4

Bình luận (0)

Dạ Thiên

15 tháng 5 2022 lúc 6:28

Đúng 2

Bình luận (2)

ONLINE SWORD ART

15 tháng 5 2022 lúc 6:48

$Đ ặ t f (x)= a.cos2x+b.sinx+cosx$

$H à m f (x) x á c đ ị nh v à li ê n t ụ c tr ê n R$

$f (π /4 ) = b \sqrt2 /2 + \sqrt2 /2$

$f ( 5/ π 4 ) = - b \sqrt 2/ 2 - \sqrt 2/ 2$

$\Rightarrow f (π /4) . f ( 5 π / 4 ) = - 1/2 ( b + 1 )^ 2 \leq 0 ; \forall a ; b ; c$

$\Rightarrow f (x) = 0 l u ô n c ó í t n h ấ t 1 n g h i ệ m t h u ộ c đ o ạ n [π / 4; 5 π / 4]$

Hay pt đã có nghiệm.

Đúng 0

Bình luận (2)

Pham Trong Bach

28 tháng 6 2019 lúc 17:55

Tính S là tổng tất cả các nghiệm của phương trình 4( 2^2x+ 2^-2x)– 4( 2^x+ 2^-x) - 7 = 0.

A. S = 1

B. S = -1

C. S = 3

D. S = 0

Xem chi tiết

Lớp 12 Toán

Cao Minh Tâm

28 tháng 6 2019 lúc 17:56

Chọn D.

Đặt t = 2^x+ 2^-x, suy ra t²= 2^2x+ 2^-2x+ 2.

Ta có

Phương trình trở thành

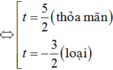
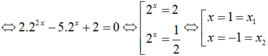
khi đó ; S = x₁+ x₂= 0.

Đúng 0

Bình luận (0)

Pham Trong Bach

30 tháng 9 2019 lúc 9:05

Cho phương trình 2 x 3 x 2 - x + 2 - 7 x 3 x 2 + 5 x + 2...

Đọc tiếp

Cho phương trình 2 x 3 x 2 - x + 2 - 7 x 3 x 2 + 5 x + 2 (1). Gọi S là tổng tất cả các nghiệm của phương trình (1). Giá trị của S là:

A. S = −11

B. S = 11

C. S = - 11 2

D. S = 11 2

Xem chi tiết

Lớp 9 Toán

Cao Minh Tâm

30 tháng 9 2019 lúc 9:06

Đáp án A

Đúng 0

Bình luận (0)

Pham Trong Bach

9 tháng 3 2019 lúc 11:38

Gọi S là tập nghiệm của phương trình 2 l o g 2 ( 2 x - 2 ) + l o g 2 ( x - 3 ) 2 2 . Tổng các phần tử của S bằng: A. 6 B. 4 + 2 C. ...

Đọc tiếp

Gọi S là tập nghiệm của phương trình 2 l o g 2 ( 2 x - 2 ) + l o g 2 ( x - 3 ) 2 = 2 . Tổng các phần tử của S bằng:

A. 6

B. 4 + 2

C. 2 + 2

D. 8 + 2

Xem chi tiết

Lớp 0 Toán

Cao Minh Tâm

9 tháng 3 2019 lúc 11:39

Chọn B

Đúng 0

Bình luận (0)

Pham Trong Bach

20 tháng 9 2018 lúc 4:49

Gọi S là tập nghiệm của phương trình 2 log 2 ( 2 x - 2 ) + log 2 ( x - 3 ) 2 2 trên ℝ . Tổng các phần tử của S là A. 8 + 2 B....

Đọc tiếp

Gọi S là tập nghiệm của phương trình 2 log 2 ( 2 x - 2 ) + log 2 ( x - 3 ) 2 = 2 trên ℝ . Tổng các phần tử của S là

A. 8 + 2

B. 4 + 2

C. 6 + 2

D. 8

Xem chi tiết

Lớp 0 Toán

Cao Minh Tâm

20 tháng 9 2018 lúc 4:50

Đúng 0

Bình luận (0)

Luyện tập 1

SGK Kết nối tri thức với cuộc sống trang 12-15

24 tháng 9 2023 lúc 10:43

Gọi S là tập nghiệm của phương trình ${x^2} - 24x + 143 = 0$.

Các mệnh đề sau đúng hay sai?

a) $13 \in S$

b) $11 \notin S$

c) $n\;(S) = 2$

Xem chi tiết

Lớp 10 Toán Bài 2: Tập hợp và các phép toán trên tập hợp

Hà Quang Minh Giáo viên CTVVIP

24 tháng 9 2023 lúc 10:47

a) Vì ${13^2} - 24.13 + 143 = 0$ nên $x = 13$ là nghiệm của phương trình $ \Rightarrow 13 \in S$

Vậy mệnh đề “$13 \in S$” đúng.

b) Vì ${11^2} - 24.11 + 143 = 0$ nên $x = 11$ là nghiệm của phương trình $ \Rightarrow 11 \in S$

Vậy mệnh đề “$11 \notin S$” sai.

c) Ta có:

$\begin{array}{l}{x^2} - 24x + 143 = 0\\ \Leftrightarrow {x^2} - 11x - 13x + 11.13 = 0\\ \Leftrightarrow x.\left( {x - 11} \right) - 13.\left( {x - 11} \right) = 0\\ \Leftrightarrow \left( {x - 11} \right).\left( {x - 13} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 11\\x = 13\end{array} \right.\end{array}$

Tập nghiệm của phương trình là $S=\{11;13\}$

Phương trình có 2 nghiệm hay $n\;(S) = 2$

=> Mệnh đề “$n\;(S) = 2$” đúng.

Đúng 0

Bình luận (0)

Nhật Anh

23 tháng 12 2021 lúc 20:33

Câu 30. Cho thuật toán tính tổng s -1+2-3+4+…+n(-1)n sử dụng phương pháp liệt kê dưới đây:Bước 1: Nhập NBước 2: i ← 0, s← 1;Bước 3: i ← i+1Bước 4: Nếu i N thì đưa ra tổng s và kết thúc chương trình.Bước 5: Nếu i chia hết cho 2 thì s ← s+i, quay lại B3Bước 6: Nếu i không chia hết cho 2 thì s ← s-i, quay lại B3Hãy cho biết bước sai trong thuật toán trên:A. Bước 2B. Bước 3C. Bước 4D. Bước 5 Câu 31: . Cho dãy a 2 4 7 6 8 9 5 12 13 3. Hỏi sau khi thực hiện xong thuật toán...

Đọc tiếp

Câu 30. Cho thuật toán tính tổng s= -1+2-3+4+…+n(-1)n sử dụng phương pháp liệt kê dưới đây:

Bước 1: Nhập N

Bước 2: i ← 0, s← 1;

Bước 3: i ← i+1

Bước 4: Nếu i > N thì đưa ra tổng s và kết thúc chương trình.

Bước 5: Nếu i chia hết cho 2 thì s ← s+i, quay lại B3

Bước 6: Nếu i không chia hết cho 2 thì s ← s-i, quay lại B3

Hãy cho biết bước sai trong thuật toán trên:

A. Bước 2

B. Bước 3

C. Bước 4

D. Bước 5

Câu 31: . Cho dãy a = 2 4 7 6 8 9 5 12 13 3.

Hỏi sau khi thực hiện xong thuật toán s = ?

B1: i ← 1 , s ← 0

B2: Nếu i > 10 thì đưa ra s rồi kết thúc

B3: s ← s + ai

B4:

4.1: Nếu ai chia hết cho 2 thì i ← i + 1

4.2: i ← i + 2

B5: Quay lại B2

A. 10

B. 20

C. 16

D. Chương trình lỗi

Câu 32: Cho dãy a = 5 7 3 11 4 6 2 8. Cho biết giá trị x sau khi thực hiện xong thuật toán?

B1: i ← 1, x ← 0

B2: Nếu i > 8 thì đưa ra x rồi kết thúc

B3:

3.1: Nếu i chia hết cho 2 thì x ← x + ai. Trái lại x ← x - ai

3.2: i ← i + 1 , quay lại B2

A. Tính hiệu a-b

B. Tính giá trị tuyệt đối của a-b

C. Tính hiệu b-a

D. Trả ra số 4,8

Câu 33: Cho n = 7; k = 4; a = 10 8 7 20 12 6 1.

Hỏi sau khi thực hiện xong thuật toán T = ?

B1: Nhập k, n, và dãy a1, a2, … an,

B2: T ← 0

B3: Nếu i > n đưa ra T rồi kết thúc

B4: Nếu ai chia hết cho k thì T ← T + ai

B5: i ← i + 1, quay lại B3

A. 1

B. 0

C. Không hiển thị gì

Chọn đáp án và sửa lại chỗ sai

Xem chi tiết

Lớp 10 Tin học

Nguyễn Lê Phước Thịnh CTV

24 tháng 12 2021 lúc 0:51

Câu 30: A

Đúng 0

Bình luận (0)

Pham Trong Bach

23 tháng 9 2019 lúc 7:36

Cho phương trình 1 2 log 2 ( x + 2 ) + x + 3 log 2 2 x + 1 x + ( 1 + 1 x )...

Đọc tiếp

Cho phương trình 1 2 log 2 ( x + 2 ) + x + 3 = log 2 2 x + 1 x + ( 1 + 1 x ) 2 + 2 x + 2 , gọi S là tổng tất cả các nghiệm dương của nó. Khi đó, giá trị của S là

A. S = - 2

B. S = 1 - 13 2

C. S = 1 + 13 2

D. Đáp án khác

Xem chi tiết

Lớp 0 Toán

Cao Minh Tâm

23 tháng 9 2019 lúc 7:37

Đúng 0

Bình luận (0)

Pham Trong Bach

11 tháng 1 2017 lúc 10:46

Cho phương trình 1 2 log 2 ( x + 2 ) + x + 3 log 2 2 x + 1 2 + ( 1 + 1 x )...

Đọc tiếp

Cho phương trình 1 2 log 2 ( x + 2 ) + x + 3 = log 2 2 x + 1 2 + ( 1 + 1 x ) 2 + 2 x + 2 , gọi S là tổng tất cả các nghiệm dương của nó. Khi đó, giá trị của S là

A. S = -2

B. S = 1 - 13 2

C. S = 1 + 13 2

D. Đáp án khác

Xem chi tiết

Lớp 12 Toán

Cao Minh Tâm

11 tháng 1 2017 lúc 10:48

Đúng 0

Bình luận (0)

KHANH QUYNH MAI PHAM

15 tháng 5 2020 lúc 21:41

Cho phương trình

$\left(m-1\right)x^2-2\left(m-3\right)x+m+1$1=0

Với điều kiện của m để phương trình có 2 nghiệm x1, x2, gọi S và P lần lượt là tổng và tích của 2 nghiệm của phương trình. Tìm các giá trị của m để S và P là các số nguyên

Xem chi tiết

Lớp 9 Toán Câu hỏi của OLM

Phạm Thị Mai Anh

21 tháng 5 2020 lúc 18:23

ư365jn5yb

Đúng 0

Bình luận (0)

Khách vãng lai đã xóa

Câu hỏi

Khoá học trên OLM (olm.vn)