Có bao nhiêu cặp số thực (x; y) sao cho x + 1 y , x y và x - 1 y là số đo ba góc một tam giác (tính theo rad) và sin 2 x + 1 y = sin 2 x y + sin 2 x - 1 y
A. 4.
B. 1.
C. 3.
D. 2.
Những câu hỏi liên quan
Có bao nhiêu cặp số thực (a;b) để trong khai triển
(
x
+
a
)
3
(
x
-
b
)
6
, hệ số của
x
7
là -9 và không có số hạng chứa
x
8
. A. 2. B. 1. C. 0. D. 4.
Đọc tiếp
Có bao nhiêu cặp số thực (a;b) để trong khai triển ( x + a ) 3 ( x - b ) 6 , hệ số của x 7 là -9 và không có số hạng chứa x 8 .
A. 2.
B. 1.
C. 0.
D. 4.
12 tháng 5 2022 lúc 21:25
Cho x là số nguyên dương và y là số thực. Có tất cả bao nhiêu cặp số \(\left(x;y\right)\) thỏa mãn \(ln\left(1+x+2y\right)=2y+3x-10\) ?
Có bao nhiêu số thực m để tôn tại duy nhất cặp số thực (x;y) thỏa mãn đồng thời
log
x
2
+
y
2
+
2
4
x
+
4
y
+
m
2
-...
Đọc tiếp
Có bao nhiêu số thực m để tôn tại duy nhất cặp số thực (x;y) thỏa mãn đồng thời log x 2 + y 2 + 2 4 x + 4 y + m 2 - m - 5 ≥ 1 và x 2 + y 2 + 2 x - 4 x + 1 = 0 .
A. 2.
B. 6.
C. 4.
D. 0.
Có bao nhiêu cặp số nguyên (a;b) với
a
,
b
∈
0
;
10
để phương trình
x
2
+
a
x
+
b
2
+
a
x
2...
Đọc tiếp
Có bao nhiêu cặp số nguyên (a;b) với a , b ∈ 0 ; 10 để phương trình x 2 + a x + b 2 + a x 2 + a x + b + b = x có bốn nghiệm thực phân biệt.
A.33
B. 32
C. 34
D. 31
Có bao nhiêu cặp số thực (x; y) sao cho (x+1)y, xy và (x-1)y là số đo ba góc một tam giác (tính theo rad) và
sin
2
x
+
1
y
sin
2
x
y
+
sin
2
x...
Đọc tiếp
Có bao nhiêu cặp số thực (x; y) sao cho (x+1)y, xy và (x-1)y là số đo ba góc một tam giác (tính theo rad) và sin 2 x + 1 y = sin 2 x y + sin 2 x - 1 y
A. 4
B. 1
C. 3
D. 2
Cho các số thực x y z thỏa mãn.Có bao nhiêu giá trị nguyên của z để có đúng 2 cặp (x;y) thỏa mãn đẳng thức trên:A.2B.211C.99D.4
Đọc tiếp
Cho các số thực x y z thỏa mãn
.Có bao nhiêu giá trị nguyên của z để có đúng 2 cặp (x;y) thỏa mãn đẳng thức trên:
A.2
B.211
C.99
D.4
Có bao nhiêu cặp số thực (x; y) sao cho (x+1)y, xy và (x-1)y là số đo ba góc một tam giác (tính theo rad) và
sin
2
[
(
x
+
1
)
y
]
sin
2
(
x
y
)
+
sin
2
[
(
x
-
1
)...
Đọc tiếp
Có bao nhiêu cặp số thực (x; y) sao cho (x+1)y, xy và (x-1)y là số đo ba góc một tam giác (tính theo rad) và sin 2 [ ( x + 1 ) y ] = sin 2 ( x y ) + sin 2 [ ( x - 1 ) y ]
A. 4.
B. 1
C. 3.
D. 2.
Đáp án B
Theo giả thiết có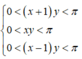 
và
Và thay vào đẳng thức điều kiện có:
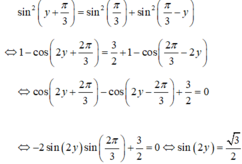
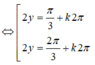
Đối chiếu với điều kiện nhận 
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu cặp số thực (x; y) thỏa mãn đồng thời các điều kiện
3
x
2
-
2
x
-
3
-
log
3
5
5
-...
Đọc tiếp
Có tất cả bao nhiêu cặp số thực (x; y) thỏa mãn đồng thời các điều kiện 3 x 2 - 2 x - 3 - log 3 5 = 5 - ( y + 4 ) và 4 y - y - 1 + y + 3 2 ≤ 8 ?
A. 3
B. 2
C. 1
D. 4
Chọn B.
Với 
,
xét từng TH phá dấu trị tuyệt đối, ta tìm được nghiệm
-3 ≤ y ≤ 0
Khi đó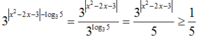 
và 
Do đó
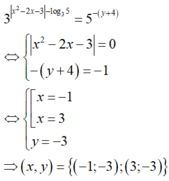
Vậy có tất cả hai cặp số thực (x; y) thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu cặp số thực (x,y) thỏa mãn đồng thời các điều kiện
3
x
2
-
2
x
-
3
-
log
3
5
5
-...
Đọc tiếp
Có tất cả bao nhiêu cặp số thực (x,y) thỏa mãn đồng thời các điều kiện 3 x 2 - 2 x - 3 - log 3 5 = 5 - y + 4 và 4 y - y - 1 + y + 3 2 ≤ 8 ?
A. 3
B. 2
C. 1
D. 4
Đáp án B.
Với 4 y - y - 1 + y + 3 2 ≤ 8 , xét từng TH phá giá trị tuyệt đối, ta tìm được nghiệm - 3 ≤ y ≤ 0 .
Khi đó 3 x 2 - 2 x - 3 - log 3 5 = 3 x 2 - 2 x - 3 3 log 3 5 = 3 x 2 - 2 x - 3 5 ≥ 1 5 và y ∈ - 3 ; 0 ⇔ y + 4 ∈ 1 ; 4 ⇒ 5 - y + 4 ≤ 5 - 1 = 1 5 .
Do đó 3 x 2 - 2 x - 3 - log 3 5 = 5 - y + 4 ⇔ [ x = - 1 x = 3 y = - 3 ⇒ x ; y = - 1 ; - 3 ; 3 ; - 3 .
Vậy có tất cả hai cặp số thực (x;y) thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)