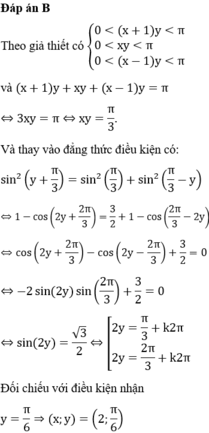Các câu hỏi tương tự
Có bao nhiêu cặp số thực (x; y) sao cho
x
+
1
y
,
x
y
và
x
-
1
y
là số đo ba góc một tam giác (tính theo rad) và
sin
2
x
+
1
y...
Đọc tiếp
Có bao nhiêu cặp số thực (x; y) sao cho x + 1 y , x y và x - 1 y là số đo ba góc một tam giác (tính theo rad) và sin 2 x + 1 y = sin 2 x y + sin 2 x - 1 y
A. 4.
B. 1.
C. 3.
D. 2.
Có bao nhiêu cặp số thực (x;y) thỏa mãn: ba số 4x-2y, 3x+y, x+6y theo thứ tự lập thành một cấp số cộng và ba số (y+2)2, xy-1, (x+1)2 theo thứ tự lập thành cấp số nhân
A. 1
B. 2
C. 3
D. 0
Cho các mệnh đề sau đây:(1) Hàm số
f
(
x
)
log
2
2
x
-
log
2
x
4
+
4
có tập xác định
D
[
0
;
+
∞
)
(2) Hàm số
y
log
a
x
có tiệm cận ngang(3) Hàm số
y
log
a
x
;
...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Trong các hàm số
y
tan
x
;
y
sin
2
x
;
y
sin
x
;
y
c
o
t
x
có bao nhiêu hàm số thỏa mãn tính chất
f
x
+
k
π
f...
Đọc tiếp
Trong các hàm số y = tan x ; y = sin 2 x ; y = sin x ; y = c o t x có bao nhiêu hàm số thỏa mãn tính chất f x + k π = f x ; ∀ x ∈ ℝ ; k ∈ ℤ
A. 3
B. 2
C. 1
D. 4
Phương trình
4
x
-
2
x
+
1
+
2
(
2
x
-
1
)
sin
(
2
x
+
y
-
1
)
+
2
0
có nghiệm xa, yb. A.
S
π
2...
Đọc tiếp
Phương trình 4 x - 2 x + 1 + 2 ( 2 x - 1 ) sin ( 2 x + y - 1 ) + 2 = 0 có nghiệm x=a, y=b.
A. S = π 2 + k π
B. S = - π 2 + k 2 π
C. S = π 3 + k π
D. S = - π 3 + k 2 π
Cho ba số dương a, b, c theo thứ tự lập thành cấp số cộng. Giá trị lớn nhất của biểu thức
P
(
a
2
+
8
b
c
)
+
3
(
2
a
+
c
)
2...
Đọc tiếp
Cho ba số dương a, b, c theo thứ tự lập thành cấp số cộng. Giá trị lớn nhất của biểu thức P = ( a 2 + 8 b c ) + 3 ( 2 a + c ) 2 + 1 có dạng x y ( x , y ∈ N ) . Hỏi x+y bằng bao nhiêu
A. 9
B. 11
C. 13
D. 7
Cho các hàm số:
y
cos
x
,
y
sin
x
,
y
tan
x
,
y
c
o
t
x
.Trong các hàm số trên, có bao nhiêu hàm số chẵn? A. 1 B. 3 C. 2 D. 4
Đọc tiếp
Cho các hàm số: y = cos x , y = sin x , y = tan x , y = c o t x .
Trong các hàm số trên, có bao nhiêu hàm số chẵn?
A. 1
B. 3
C. 2
D. 4
Cho x,y là các số phức ta có các khẳng định sau: 1)
x
+
y
¯
v
à
x
¯
+
y
là hai số phức liên hợp của nhau. 2)
x
y
¯
v
à
x
¯
y
là hai số phức liên hợp của nhau. 3)
x
−
y...
Đọc tiếp
Cho x,y là các số phức ta có các khẳng định sau:
1) x + y ¯ v à x ¯ + y là hai số phức liên hợp của nhau.
2) x y ¯ v à x ¯ y là hai số phức liên hợp của nhau.
3) x − y ¯ v à x ¯ − y là hai số phức liên hợp của nhau.
Hỏi có bao nhiêu khẳng định đúng
A. không
B. một
C. hai
D. ba
Cho hàm số
y
f
x
có bảng biến thiên như hình vẽ bênCó bao nhiêu số nguyên dương m để phương trình
f
2
sin
x
+
1
f
(
m
)
có nghiệm thực ? A. 2. B. 5. C. 4. D. 3.
Đọc tiếp
Cho hàm số y = f x có bảng biến thiên như hình vẽ bên
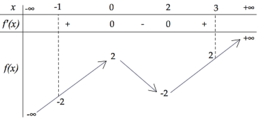
Có bao nhiêu số nguyên dương m để phương trình f 2 sin x + 1 = f ( m ) có nghiệm thực ?
A. 2.
B. 5.
C. 4.
D. 3.