Cho hệ 5 y + log 4 x = 8 3 5 y . log 4 x = - 1 Gọi x , y là nghiệm của hệ. Tìm x.
![]()
![]()
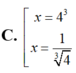
![]()
Giả sử đã cho \({\log _a}M\) và ta muốn tính \({\log _b}M.\) Để tìm mối liên hệ giữa \({\log _a}M\) và \({\log _b}M,\) hãy thực hiện các yêu cầu sau:
a) Đặt \(y = {\log _a}M,\) tính M theo y;
b) Lấy loogarit theo cơ số b cả hai vế của kết quả nhận được trong câu a, từ đó suy ra công thức mới để tính y.
a) \(y = {\log _a}M \Leftrightarrow M = {a^y}\)
b) Lấy loogarit theo cơ số b cả hai vế của \(M = {a^y}\) ta được
\({\log _b}M = {\log _b}{a^y} \Leftrightarrow {\log _b}M = y{\log _b}a \Leftrightarrow y = \frac{{{{\log }_b}M}}{{{{\log }_b}a}}\)
Cho x = log 2018, y = ln 2018. Hỏi quan hệ nào sau đây giữa x và y là đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Trên cùng một hệ trục toạ độ, vẽ đồ thị các hàm số \(y = {\log _3}x\) và \(y = {\log _{\frac{1}{3}}}x\).
Cho log3a=5 và log3b=\(\frac{2}{3}\). Tính giá trị của biểu thức y=2 log 6[log5(5a)]+\(log_{\frac{1}{9}}b^3\)
Bạn thử tải app này xem có đáp án không nhé <3 https://giaingay.com.vn/downapp.html
Cho bốn số thực dương a, b, x, y với \(a,b \ne 1\). Khẳng định nào sau đây là sai?
A. \({\log _a}(xy) = {\log _a}x + {\log _b}y\).
B. \({\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y\).
C. \({\log _a}\frac{1}{x} = \frac{1}{{{{\log }_a}x}}\).
D. \({\log _a}b \cdot {\log _b}x = {\log _a}x\).
Trong các hàm số sau, những hàm số nào là hàm số lôgarit? Khi đó hãy chỉ ra cơ số.
a) \(y = {\log _{\sqrt 3 }}x;\)
b) \(y = {\log _{{2^{ - 2}}}}x;\)
c) \(y = {\log _x}2;\)
d) \(y = {\log _{\frac{1}{x}}}5.\)
Hàm số a,b là các hàm số logarit
a: \(log_{\sqrt{3}}x\)
Cơ số là \(\sqrt{3}\)
b: \(log_{2^{-2}}x\)
Cơ số là \(2^{-2}=\dfrac{1}{4}\)
Cho a,b là các số thực thỏa mãn log 2 . log 2 a - log b = 2 . Hỏi a,b thỏa mãn hệ thức nào dưới đây?
A. a = 100b
B. a = 100 - b
C. a = =100 + b
D. a = 100 b
Cho các số thực dương x, y ≠ 1 và thoả mãn logxy=logyx, logx(x-y)=logy(x+y). Giá trị của x2+xy+y2bằng:
ĐKXĐ: \(x\ne y\)
\(log_xy=\frac{1}{log_xy}\Leftrightarrow log_x^2y=1\Leftrightarrow\left[{}\begin{matrix}log_xy=1\\log_xy=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=y\left(l\right)\\x=\frac{1}{y}\end{matrix}\right.\)
\(log_x\left(x-\frac{1}{x}\right)=log_{x^{-1}}\left(x+\frac{1}{x}\right)\Leftrightarrow log_x\left(x-\frac{1}{x}\right)=-log_x\left(x+\frac{1}{x}\right)\)
\(\Leftrightarrow log_x\left(x-\frac{1}{x}\right)\left(x+\frac{1}{x}\right)=0\Leftrightarrow\left(x-\frac{1}{x}\right)\left(x+\frac{1}{x}\right)=1\)
\(\Leftrightarrow x^2-\frac{1}{x^2}=1\Leftrightarrow x^4-x^2-1=0\Rightarrow x^2=\frac{1+\sqrt{5}}{2}\Rightarrow y^2=\frac{1}{x^2}=\frac{-1+\sqrt{5}}{2}\)
\(\Rightarrow x^2+xy+y^2=\frac{1+\sqrt{5}}{2}+1+\frac{-1+\sqrt{5}}{2}=\sqrt{5}+1\)
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()
Cho các số thực dương x, y ≠ 1 và thoả mãn logxy=logyx, logx(x-y)=logy(x+1). Giá trị của x2+xy+y2 bằng:
\(log_xy=log_yx=\frac{1}{log_xy}\Rightarrow\left(log_xy\right)^2=1\Rightarrow\left[{}\begin{matrix}log_xy=1\\log_xy=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=y\\x=\frac{1}{y}\end{matrix}\right.\)
Do \(log_x\left(x-y\right)\) tồn tại \(\Rightarrow x-y\ne0\Rightarrow x\ne y\Rightarrow x=\frac{1}{y}\)
\(log_x\left(x-y\right)=log_y\left(x+1\right)\Leftrightarrow log_x\left(x-\frac{1}{x}\right)=-log_x\left(x+1\right)\)
\(\Leftrightarrow log_x\left[\left(x-\frac{1}{x}\right)\left(x+1\right)\right]=0\Leftrightarrow\left(x-\frac{1}{x}\right)\left(x+1\right)=1\)
\(\Leftrightarrow\left(x^2-1\right)\left(x+1\right)=x\Leftrightarrow x^3+x^2-2x-1=0\)
Pt này nghiệm xấu, đề bài có vấn đề