Thể tích của khối cầu có bán kính r = 1 2 là
A. V = π 2 3
B. V = π 2 4
C. V = π 2
D. V = π 2 2
Mặt cầu bán kính r có diện tích bằng 36 π . Tìm thể tích V của khối cầu bán kính r.
A. V = 72 2 π
B. V = 288 π
C. V = 36 π
D. V = 18 π
Cho một mặt cầu có diện tích S, thể tích khối cầu đó là V. Bán kính R của mặt cầu là:
A. R = 4V/S B. R = S/3V
C. R = 3V/S D. R = V/3S
Chọn C.
Dựa vào công thức diện tích mặt cầu và thể tích hình cầu, ta có:
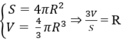
Cho khối cầu có thể tích V = 4 πa 3 (a > 0). Tính theo a bán kính R của khối cầu.
A. R = a 3 3
B. R = a 2 3
C. R = a 4 3
D. R = a
Bán kính r của khối cầu có thể tích V = 36 π c m 3 là
A. 3 cm
B. 6 cm
C. 4 cm
D. 9 cm
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
A. R = 3 V S
B. R = S 3 V
C. R = 4 V S
D. R = V 3 S
Chọn A.
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là:
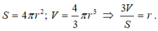
Công thức tính thể tích V của khối cầu có bán kính bằng R là
A. V = 4 πR 2
B. V = 4 3 πR 2
C. V = 4 3 πR 3
D. V = πR 3
Công thức tính thể tích V của khối cầu có bán kính bằng R là
A. V = 4 π R 2
B. V = 4 3 π R 2
C. V = 4 3 π R 3
D. V = π R 3
Khối lượng riêng của thép là \(7850kg\)/m3. Tính khối lượng của một quả cầu thép bán kính 0,15 m. Cho biết công thức tính thể tích của khối cầu là \(V=\dfrac{4}{3}\pi r^3\), với r là bán kính quả cầu.
Thể tích của quả cầu thép là:
\(V = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi .0,{15^3} = 0,014\left( {{m^3}} \right)\)
Khối lượng của quả cầu thép là:
\(m = \rho V = 7850.0,014 = 110\left( {kg} \right)\)
I. Trắc nghiệm ( 6 điểm)
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
A. R = 3 V S
B. R = S 3 V
C. R = 4 V S
D. R = V 3 S
Chọn A.
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là:
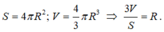
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P = R + 2r.
A. 2 3
B. 3
C. 3 3
D. 2
Đáp án D.
Khối nón cụt có thể tích là V = πh 3 R 2 + R . r + r 2 mà h = 3 V = π ⇒ R 2 + R . r + r 2 = 1 (*).
Ta có P = R + 2 r ⇔ R = P - 2 r thay vào (*), ta được P - 2 r 2 + P - 2 r r + r 2 = 1
⇔ P 2 - 4 P r + 4 r 2 + P r - 2 r 2 + r 2 - 1 = 0 ⇔ 3 r 2 - 3 P r + P 2 - 1 = 0 (I).
Vậy phương trình (I) có nghiệm khi và chỉ khi ∆ I = - 3 P 2 - 4 . 3 . P 2 - 1 ≥ 0 ⇔ P ≤ 2 .
Vậy giá trị lớn nhất của P là 2.