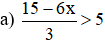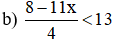Bài 1: 

a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)

\(\Leftrightarrow6-8x-10+2x-5=0\)

\(\Leftrightarrow-6x+11=0\)

\(\Leftrightarrow-6x=-11\)

hay \(x=\dfrac{11}{6}\)

b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)

\(\Leftrightarrow6-12x-11+3x-1=0\)

\(\Leftrightarrow-9x-6=0\)

\(\Leftrightarrow-9x=6\)

hay \(x=-\dfrac{2}{3}\)

1) \(\frac{x-1}{x+3}-\frac{x}{x-3}=\frac{4x+15}{9-x^2}\)

ĐKXĐ : \(x\ne\pm3\)

\(\Leftrightarrow\frac{x-1}{x+3}-\frac{x}{x-3}=\frac{-4x-15}{x^2-9}\)

\(\Leftrightarrow\frac{\left(x-1\right)\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-\frac{x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\frac{-4x-15}{\left(x-3\right)\left(x+3\right)}\)

\(\Leftrightarrow\frac{x^2-4x+3}{\left(x-3\right)\left(x+3\right)}-\frac{x^2+3x}{\left(x-3\right)\left(x+3\right)}=\frac{-4x-15}{\left(x-3\right)\left(x+3\right)}\)

\(\Leftrightarrow\frac{x^2-4x+3-x^2-3x}{\left(x-3\right)\left(x+3\right)}=\frac{-4x-15}{\left(x-3\right)\left(x+3\right)}\)

\(\Leftrightarrow-7x+3=-4x-15\)

\(\Leftrightarrow-7x+4x=-15-3\)

\(\Leftrightarrow-3x=-18\)

\(\Leftrightarrow x=6\)( tmđk )

Vậy x = 6 là nghiệm của phương trình

2) 2x + 3 < 6 - ( 3 - 4x )

<=> 2x + 3 < 6 - 3 + 4x

<=> 2x - 4x < 6 - 3 - 3

<=> -2x < 0

<=> x > 0

Vậy nghiệm của bất phương trình là x > 0

\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)

\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)

\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)

\(\Leftrightarrow x^2-9-x^2+3x=0\)

\(\Leftrightarrow3x-9=0\)

\(\Leftrightarrow3x=9\)

\(\Leftrightarrow x=3\left(n\right)\)

Vậy \(S=\left\{3\right\}\)

\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)

\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)

\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)

\(\Leftrightarrow12x-9-12x+20+2x-7>0\)

\(\Leftrightarrow2x+4>0\)

\(\Leftrightarrow2x>-4\)

\(\Leftrightarrow x>-2\)

a) \(\dfrac{15-6x}{3}>5\Leftrightarrow15-6x>15\)

\(\Leftrightarrow-6x>0\Leftrightarrow x< 0\) (vì \(-6< 0\))

\(S=\left\{x|x< 0\right\}\)

b) \(\dfrac{8-11x}{4}< 13\Leftrightarrow8-11x< 52\)

\(\Leftrightarrow-11x< -44\Leftrightarrow x>4\) (vì \(-11< 0\))

\(S=\left\{x|x>4\right\}\)

c) \(8x+3\left(x+1\right)>5x-\left(2x-6\right)\)

\(\Leftrightarrow8x+3x+1>5x-2x+6\)

\(\Leftrightarrow8x+3x-5x+2x>6-1\)

\(\Leftrightarrow8x>5\)

\(\Leftrightarrow x>\dfrac{5}{8}\) (vì \(8>0\))

\(S=\left\{x|x>\dfrac{5}{8}\right\}\)

d) \(2x\left(6x-1\right)>\left(3x-2\right)\left(4x+3\right)\)

\(\Leftrightarrow12x^2-2x>12x^2+9x-8x-6\)

\(\Leftrightarrow12x^2-2x-12x^2-9x+8x>-6\)

\(\Leftrightarrow-3x>-6\)

\(\Leftrightarrow x< 2\) (vì \(-3< 0\))

\(S=\left\{x|x< 2\right\}\)

a) \(\dfrac{15-6x}{3}>5\) <=> \(15-6x>15\) <=> \(6x< 0\) <=> \(x< 0\)

b) \(\dfrac{8-11x}{4}< 13\) <=> \(8-11x< 52\) <=> \(11x>-44\)<=> \(x>-4\)

c) \(8x+3\left(x+1\right)>5x-\left(2x-6\right)\)

<=> 8x + 3x + 3 - 5x + 2x - 6 > 0

<=> 8x  > 3

<=> x > 3/8

d) 2x(6x - 1) > (3x - 2)(4x + 3)

<=> 12x² - 2x > 12x² + x - 6

<=> 12x² - 2x - 12x² - x > -6

<=> -3x > -6

<=> x < 2

a.

\(3\sqrt{-x^2+x+6}\ge2\left(1-2x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-x^2+x+6\ge0\\1-2x< 0\end{matrix}\right.\\\left\{{}\begin{matrix}1-2x\ge0\\9\left(-x^2+x+6\right)\ge4\left(1-2x\right)^2\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-2\le x\le3\\x>\dfrac{1}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\25\left(x^2-x-2\right)\le0\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}< x\le3\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\-1\le x\le2\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow-1\le x\le3\)

b.

ĐKXĐ: \(x\ge0\)

\(\Leftrightarrow\sqrt{2x^2+8x+5}-4\sqrt{x}+\sqrt{2x^2-4x+5}-2\sqrt{x}=0\)

\(\Leftrightarrow\dfrac{2x^2+8x+5-16x}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-4x+5-4x}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)

\(\Leftrightarrow\dfrac{2x^2-8x+5}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-8x+5}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)

\(\Leftrightarrow\left(2x^2-8x+5\right)\left(\dfrac{1}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{1}{\sqrt{2x^2-4x+5}+2\sqrt{x}}\right)=0\)

\(\Leftrightarrow2x^2-8x+5=0\)

\(\Leftrightarrow x=\dfrac{4\pm\sqrt{6}}{2}\)

Câu b còn 1 cách giải nữa:

Với \(x=0\) không phải nghiệm

Với \(x>0\) , chia 2 vế cho \(\sqrt{x}\) ta được:

\(\sqrt{2x+8+\dfrac{5}{x}}+\sqrt{2x-4+\dfrac{5}{x}}=6\)

Đặt \(\sqrt{2x-4+\dfrac{5}{x}}=t>0\Leftrightarrow2x+8+\dfrac{5}{x}=t^2+12\)

Phương trình trở thành:

\(\sqrt{t^2+12}+t=6\)

\(\Leftrightarrow\sqrt{t^2+12}=6-t\)

\(\Leftrightarrow\left\{{}\begin{matrix}6-t\ge0\\t^2+12=\left(6-t\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}t\le6\\12t=24\end{matrix}\right.\)

\(\Rightarrow t=2\)

\(\Rightarrow\sqrt{2x-4+\dfrac{5}{x}}=2\)

\(\Leftrightarrow2x-4+\dfrac{5}{x}=4\)

\(\Rightarrow2x^2-8x+5=0\)

\(\Leftrightarrow...\)

\(2x+2x+1< 2x-9\)

\(\Leftrightarrow2x+1< -9\)

\(\Leftrightarrow2x< 9-1\Leftrightarrow2x< 8\)

\(\Leftrightarrow2x:2< 8:2\Leftrightarrow x< 4\)

\(4x+1< 2x-9\)

\(\Leftrightarrow4x+1-2x+9< 0\)

\(\Leftrightarrow2x+10< 0\)

\(\Leftrightarrow2x< -10\)

\(\Leftrightarrow x< -5\)

Giá trị  x = 2 là nghiệm của bất phương trình nào trong các bất phương trình nào dưới đây ?

a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta  = 529 > 0\), có hai nghiệm phân biệt \({x_1} =  - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)

Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)

b) \( - 6{x^2} + 11x > 10 \Leftrightarrow  - 6{x^2} + 11x - 10 > 0\)

Xét tam thức \(f\left( x \right) =  - 6{x^2} + 11x - 10\) có \(\Delta  =  - 119 < 0\)và có \(a =  - 6 < 0\)

Ta có bảng xét dấu như sau

Vậy bất phương trình vô nghiệm

c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)

Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta  =  - 12 < 0\)và có \(a = 2 > 0\)

Ta có bảng xét dấu như sau

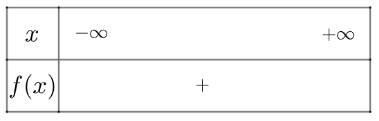
Vậy bất phương trình có vô số nghiệm

d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta  = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)

Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là \(x = 5\)