Cho P : 2 x - y + 2 z - 1 = 0 , A bất kì thuộc (P). Gọi M là trung điểm OA ( O là gốc tọa độ). Tính khoảng cách h từ M tới mặt phẳng (P).
![]()
![]()
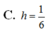
![]()
Trong không gian Oxyz cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 2 ) 2 = 4 và mặt phẳng (P): x-y+2z-1=0 Gọi M là một điểm bất kì trên mặt cầu (S) Khoảng cách từ M đến (P) có giá trị nhỏ nhất bằng
![]()
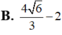
![]()
![]()
Trong không gian Oxyz, cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 2 ) 2 = 4 và mặt phẳng (P): x-y+2z-1=0. Gọi M là một điểm bất kì trên mặt cầu (S). Khoảng cách từ M đến (P) có giá trị nhỏ nhất bằng
A. 4 6 3 - 2
B. 0
C. 6 - 2
D. 2 6 - 2
1. Cho tam giác ABC đều. Có đường cao bằng 3cm. Gọi M là điểm bất kì nằm trong tam giá. Gọi x, y, z là khoảng cách từ M đến AB, BC, AC.
Tìm min \(x^2+y^2+z^2\)
2. Cho điểm O nằm trong tam giác ABC. Tia AO cắt BC tại A' ; BO cắt AC tại B' ; CO cắt AB tại C'. CMR: \(\dfrac{OA'}{AA'}+\dfrac{OB'}{BB'}+\dfrac{OC'}{CC'}=1\)
1.
Gọi cạnh tam giác ABC là a
\(S_{ABC}=S_{AMB}+S_{BMC}+S_{AMC}\\ \Leftrightarrow\dfrac{1}{2}ah=\dfrac{1}{2}ax+\dfrac{1}{2}ay+\dfrac{1}{2}az\\ \Leftrightarrow x+y+z=h\)
Lại có \(3\left(x^2+y^2+z^2\right)\ge\left(x+y+z\right)^2=h^2\left(bunhia\right)\)
\(\Leftrightarrow x^2+y^2+z^2\ge\dfrac{1}{3}h^2\)
Dấu \("="\Leftrightarrow x=y=z\Leftrightarrow M\) là giao 3 đường p/g của \(\Delta ABC\)
Cho ( P ) : y = x 2 , A ( - 2 ; 1 2 ) . Gọi M là một điểm bất kì thuộc (P). Khoảng cách MA bé nhất là
A. 5 2
B. 2 3 3
C. 2 2
D. 5 4
cho tam giác abc đều. đường cao AH có độ dài = 3. M là một điểm bất kì năm trong tam giác. Gọi x;y;z lần lượt là khoảng cách từ M đến cạnh BC,CA,AB. Xác định điểm M để bthức E = x^2 + y^2 + z^2 đạt GTNN
1. Tìm x biết : (x+3).(x-7)<0
2. Cho 16 số nguyên.Tích của 3 số bất kì luôn là số âm.Chứng minh rằng tích của 16 số đó là dương.
3. Tìm x, y thuộc Z biết :
a)xy+3x=21+7y
b)xy+3x-2y=11
bài 1.suy ra (x-7)(x+3) là số âm
suy ra x-7 và x+3 là 2 số trái dấu
mà x+3>x-7
suy ra: x+3 >0 suy ra x> -3
x-7<7 suy ra x<7
suy ra x thuộc {-2;-1;0;1;2;3;4;5;6}
Cho parabol (P): \(y = \frac{1}{4}{x^2}\). Xét F(0; 1) và đường thẳng\(\Delta :{\rm{ }}y{\rm{ }} + 1 = 0\) . Với điểm M(x;y) bất kì, chứng minh rằng \(MF{\rm{ }} = \;d\left( {M,\Delta } \right) \Leftrightarrow \) M(xy) thuộc (P).
Ta có: \(MF = \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} ,d\left( {M,\Delta } \right) = \left| {y + 1} \right|\).
Xét \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} = \left| {y + 1} \right| \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} = {\left( {y + 1} \right)^2} \Leftrightarrow {x^2} = 4y \Leftrightarrow y = \frac{1}{4}{x^2}\).
Vậy tập hợp điểm M để \(MF{\rm{ }} = \;d\left( {M,\Delta } \right)\) là parabol \(y = \frac{1}{4}{x^2}\)
Trong không gian Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 9 và mặt phẳng (P): 2x-2y+z+14=0. Gọi M ( a ; b ; c ) là điểm thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) lớn nhất. Tính T = a + b + c .
![]()
![]()
![]()
![]()
cho (O:R) đk AB cố định gọi H là điểm bất kì thuộc OA vẽ dây CD vuông góc vs AB tại H gọi M là điểm bất kì thuộc CH nối AM cắt (O) tại điểm thứ 2 là E tia BE cắt DC tại F
a cm H,M,B,E cùng thuộc 1 đg trong
b kẻ Ex là tia đối cuae ED cm ∠FEx =∠FEC và MC>FD= FC.MC
c