Cho hình lăng trụ đứng ABC.A’B’C’ có AB=1,AC=2,AA’=3 và B A C ^ = 120 ∘ Gọi M, N lần lượt là các điểm trên cạnh BB’,CC’ sao cho BM=3B’M,CN=2C’N Tính khoảng cách từ điểm M đến mặt phẳng (A’BN)
A. 9 138 184
B. 3 138 46
C. 9 3 16 46
D. 9 138 46
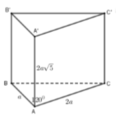
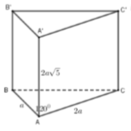
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác với A B = a , A C = 2 a và B A C ^ = 120 ° , A A ' = 2 a 5 . Tính thể tích V của khối lăng trụ đã cho.
A. V = a 3 15
B. V = 4 a 3 5 3
C. V = a 3 15 3
D. V = 4 a 3 5
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác với AB=a, AC=2a và B A C = 120 ° , A A ' = 2 a 5 . Tính thể tích V của khối lăng trụ đã cho.
A. V = a 3 15
B. V = 4 a 3 5 3
C. V = a 3 15 3
D. 4 a 3 5
Diện tích tam giác ABC là:
S A B C = 1 2 A B . A C . sin A = 1 2 a . 2 a . 3 2 = a 2 3 2
Thể tích lăng trụ
V = S A B C . A A ' = a 3 3 2 . 2 a 5 = a 3 15
Chọn đáp án A.
Cho hình lăng trụ đứng ABC.A’B’C’ có AB=1, AC=2, B A C ^ = 120 ° . Giả sử D là trung điểm của cạnh CC’ và B D A ^ = 90 ° . Tính thể tích V của khối lăng trụ ABC.A’B’C’
A. V = 15 2
B. V = 3 15
C. V = 3 15 7
D. V = 2 15
Cho hình lăng trụ đứng ABC.A’B’C’ có tam giác ABC vuông tại A, AB = AA’ = a, AC = 2a. Tính thể tích khối lăng trụ đã cho.
![]()
B. a3
C. 2a3
![]()
Cho hình lăng trụ đứng ABC.A’B’C’ có AB=1,AC=2,AA’=3và B A C ^ = 120 ∘ . Gọi M,N lần lượt là các điểm trên cạnh BB’, CC’ sao cho BM=3B’M,CN=2C’N. Tính khoảng cách từ điểm M đến mặt phẳng (A’BN).
A. 9 3 16 46
B. 9 138 46
C. 9 138 184
D. 3 138 46
Cho hình lăng trụ đứng ABC.A’B’C’ có ΔABC vuông cân tại B, AB = a 2 và cạnh bên AA’ = a 6 . Khi đó diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ đứng đã cho là:
A. 4πa2
B. 2 πa 2 6
C. 4 πa 2 6
D. πa 2 6
Chọn B.
Bán kính của đường tròn ngoại tiếp tam giác đáy R = a
S xq = a 6 . 2 πR = 2 πa 2 6
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, A B = 2 3 , B C = a , A A ' = 3 a 2 . Khoảng cách giữa hai đường thẳng AC’ và B’C bằng
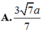
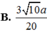
![]()
![]()
Câu 18: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a:
\(A,\sqrt{3a^3}\) \(B,\dfrac{\sqrt{3a^3}}{6}\) \(C,\dfrac{\sqrt{3a^3}}{2}\) \(D,2a^3\)
\(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.a.a\sqrt{3}=\dfrac{a^2\sqrt{3}}{2}\)
\(\Rightarrow V_{ABC}.A'B'C'=AA'.S_{ABC}=2a.\dfrac{a^2\sqrt{3}}{2}=a^3\sqrt{3}\)
Chọn A
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác với AB = a, AC = 2a và BAC = 120 0 , A A ' = 2 a 5 . Tính thể tích V của khối lăng trụ đã cho.
A. V = a 3 15
B. V = 4 a 3 5 3
C. V = a 3 15 3
D. V = 4 a 3 5
Phương pháp:
Thể tích lăng trụ V = Bh với B là diện tích đáy, h là chiều cao.
Diện tích tam giác ABC là:
![]()
Thể tích lăng trụ
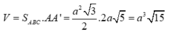
Chọn A.