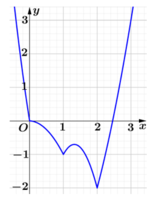
Cho hàm số f(x) liên tục trên đoạn [0;3] và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên [0;3]. Giá trị của M + m bằng ?
A. 5
B. 3
C. 2
D. 1
Những câu hỏi liên quan
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
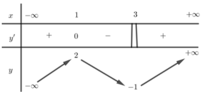
Số nghiệm của phương trình f(x) + 1 = 0 là:
A. 3.
B. 0.
C. 1.
D. 2.
Quan sát bảng biến thiên ta thấy phương trình này có 2 nghiệm.
Chọn D
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số yf’(x),(yf’(x) liên tục trên R). Xét hàm số
g
x
f
x
2
-
2
. Mệnh đề nào dưới đây sai? A. Hàm số g(x) nghịch biến trên (-∞;-2). B. Hàm số g(x) đồng biến trên (2;+∞). C. Hàm số g(x)nghịch biến trên(-1;0). D. Hàm số g(x) ngh...
Đọc tiếp
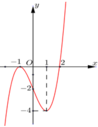
Cho hàm số y=f(x) có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số y=f’(x),(y=f’(x) liên tục trên R). Xét hàm số g x = f x 2 - 2 . Mệnh đề nào dưới đây sai?
A. Hàm số g(x) nghịch biến trên (-∞;-2).
B. Hàm số g(x) đồng biến trên (2;+∞).
C. Hàm số g(x)nghịch biến trên(-1;0).
D. Hàm số g(x) nghịch biến trên (0;2).
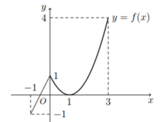
Cho hàm số f(x) liên tục trên [-1;3] và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên [-1;3]. Tính M - m.
A. 3
B. 4
C. 5
D. 1
Chọn C
Quan sát đồ thị ta thấy hàm số y = f(x) đạt giá trị nhỏ nhất trên [-1;3] là -1 tại điểm x = =-1 và đạt giá trị lớn nhất trên[-1;3] là 4 tại điểm x = 3. Do đó M = 4, m = -1.
Giá trị M - m = 4 - (-1) = 5.
Đúng 0
Bình luận (0)
Cho hàm số y f(x) liên tục trên R và thỏa mãn f(-1)0f(x) Gọi S là diện tích hình phẳng giới hạn bởi các đường yf(x); y0; x-1 và x1Mệnh đề nào sau đây đúng?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và thỏa mãn f(-1)>0<f(x) Gọi S là diện tích hình phẳng giới hạn bởi các đường y=f(x); y=0; x=-1 và x=1Mệnh đề nào sau đây đúng?
Cho hàm số yf(x) liên tục trên R và thỏa mãn f(-1)0f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường yf(x),y0,x-1 và x1. Mệnh đề nào sau đây đúng? A.
S
∫
-
1
0
f
(
x
)
d
x
+
∫
0
1
|
f
(
x
)
|
d
x...
Đọc tiếp
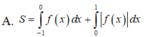
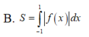
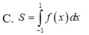
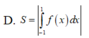
Cho hàm số y=f(x) liên tục trên R và thỏa mãn f(-1)>0<f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y=f(x),y=0,x=-1 và x=1. Mệnh đề nào sau đây đúng?
A. S = ∫ - 1 0 f ( x ) d x + ∫ 0 1 | f ( x ) | d x
B. S = ∫ - 1 1 | f ( x ) | d x
C. S = ∫ - 1 1 f ( x ) d x
D. S = ∫ - 1 1 f ( x ) d x
Cho hàm số y f(x) liên tục trên R và thỏa mãn
∫
1
e
f
(
ln
x
)
x
d
x
e
. Mệnh đề nào sau đây là đúng?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và thỏa mãn ∫ 1 e f ( ln x ) x d x = e . Mệnh đề nào sau đây là đúng?
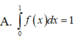
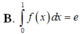
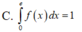
Giả sử F(x) là nguyên hàm của hàm số f(x)
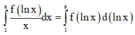
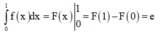
Đáp án B
Đúng 0
Bình luận (0)
Cho hàm số yf(x) liên tục trên R và thỏa mãn
∫
1
e
f
(
ln
x
)
x
d
x
e
. Mệnh đề nào sau đây là đúng? A.
∫
0
1
f
(
x
)
d
x
1
B.
∫...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và thỏa mãn ∫ 1 e f ( ln x ) x d x = e . Mệnh đề nào sau đây là đúng?
A. ∫ 0 1 f ( x ) d x = 1
B. ∫ 0 1 f ( x ) d x = e
C. ∫ 0 e f ( x ) d x = 1
D. ∫ 0 e f ( x ) d x = e
Cho hàm số
y
f
x
liên tục trên
ℝ
. Biết đồ thị của hàm số
y
f
x
như hình vẽ Số điểm cực trị của hàm số
y
f
x
là
Đọc tiếp
Cho hàm số y = f x liên tục trên ℝ . Biết đồ thị của hàm số y = f ' x như hình vẽ
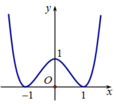
Số điểm cực trị của hàm số y = f x là
Bài 1: xét tính liên tục của hàm số
g(x)=\(\left\{{}\begin{matrix}\dfrac{x^2-3x+2}{x^3-8}khix< 2\\x+1khix\ge2\end{matrix}\right.\)tại x0=2
Bài 2: Tìm a để hàm số sau liên tục trên R:
g(x)= \(\left\{{}\begin{matrix}\dfrac{\sqrt{3x-2}-2}{x-2}khix>2\\ax-1khix\le2\end{matrix}\right.\)tại x0=2
1/ \(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\left(x+1\right)=f\left(2\right)=3\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{\left(x-2\right)\left(x-1\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\lim\limits_{x\rightarrow2^-}\dfrac{x-1}{x^2+2x+4}=\dfrac{1}{12}\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=f\left(2\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\)
=> ham so gian doan tai x=2
2/ \(\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)=2a-1\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{3x-2-4}{\left(x-2\right)\left(\sqrt{3x-2}+2\right)}=\lim\limits_{x\rightarrow2^+}\dfrac{3}{\sqrt{3x-2}+2}=\dfrac{3}{4}\)
De ham so lien tuc tai x=2
\(\Leftrightarrow\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)=\lim\limits_{x\rightarrow2^+}f\left(x\right)\Leftrightarrow2a-1=\dfrac{3}{4}\Leftrightarrow a=\dfrac{7}{8}\)
Đúng 2
Bình luận (0)