Cho hàm số y = x 3 + 6 x 2 + 12 x + 8 có đồ thị (C). Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên R.
B. Đồ thị (C) tiếp xúc với trục hoành.
C. Phương trình ![]() có một nghiệm với mọi m.
có một nghiệm với mọi m.
D. Hàm số đạt cực trị tại ![]()
Cho hàm số y=f(x)=2/3.x
a) Tìm f(7); f(-5/4)
b)Tìm x khi y=10
c)Tìm x khi f(x)=8
d)Vẽ đồ thị hàm số trên.
e) Hỏi điểm P(9;16) có thuộc đồ thị hàm số y=2/3 x ko?
g) Tìm điểm K và H trên đồ thị hàm số y=2/3x biết xK =6,yH =4.
Cho hàm số y=f(x)=3X
a, Vẽ đồ thị hàm số
b, Tính f(5); f(-7/12)
c, Các điểm M( -2:6), C( 4/9; 4/3) có thuộc đồ thị hàm số không ? Vì sao
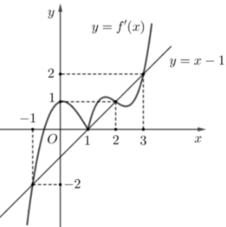
Cho hàm số y= f( x) và đồ thị hình bên là đồ thị của hàm y= f’ ( x) . Hỏi đồ thị của hàm số g ( x ) = 2 f ( x ) - x - 1 2 có tối đa bao nhiêu điểm cực trị ?

A. 6.
B. 7.
C. 8.
D. 9.
Đặt h( x) = 2f( x) – ( x-1) 2
Suy ra đạo hàm: h’( x) = 2f’(x) -2( x-1).
Ta vẽ thêm đường thẳng y= x-1.
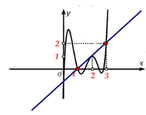
Ta có h’ (x) =0 khi f’(x) =x-1
Suy ra x=0; x=1; x=2; x=3
Theo đồ thị h’(x) > .0 khi f’(x) > x-1
Ta có :

Đồ thị hàm số g( x) có nhiều điểm cực trị nhất khi h( x) có nhiều giao điểm với trục hoành nhất.
Vậy đồ thị hàm số h( x) cắt trục hoành tại nhiều nhất 4 điểm, suy ra đồ thị hàm số g(x) có tối đa 7 điểm cực trị.
Chọn B.
Bài 1:Cho hàm số y = f(x)=a/x a) biết điểm M (6;6) thuộc đồ thị hàm số. Xác định a b) điểm nào trong các điểm sau thuộc đồ thị hàm số ? A.(-1;-6) B.(1/2;10) C.(-1/2;-12) D.(-1/3;-3)
Lời giải:
Vì $M\in (y=\frac{a}{x})$ nên:
$y_M=\frac{a}{x_M}\Rightarrow a=x_M.y_M=6.6=36$
Vậy hàm số có công thức $y=\frac{36}{x}(*)$
Giờ bạn thay tung độ (y) và hoành độ (x) của từng điểm vô xem có đúng với $(*)$ không thì thu được không có điểm nào thuộc ĐTHS.
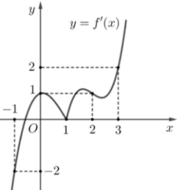
Cho hàm số y=f(x) có đạo hám liên tục trên R và có đồ thị f '(x) như hình vẽ bên. Biết rằng f - 3 > 8 , f 2 < 1 2 , f 4 > 9 2 Số điểm cực trị của hàm số y = f ( x ) - x - 1 2 2 là
A. 7
B. 5
C. 8
D. 6
Xét 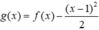 có
có
![]()
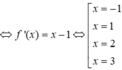
Vì đường thẳng y=x-1 cắt đồ thị f '(x) tại 4 điểm có hoành độ x=-1, x=1, x=2, x=3

Suy ra g(x) có ba điểm cực trị là x=-1, x=1, x=2, x=3
Theo giả thiết  có nên g(x)=0 có hai nghiệm phân biệt (là nghiệm đơn hoặc bội lẻ). Vậy hàm số y=|g(x)| có tổng cộng 3 + 2 = 5 điểm cực trị.
có nên g(x)=0 có hai nghiệm phân biệt (là nghiệm đơn hoặc bội lẻ). Vậy hàm số y=|g(x)| có tổng cộng 3 + 2 = 5 điểm cực trị.
Chọn đáp án B.
*Chú ý số điểm cực trị của hàm số y=|g(x)| bằng tổng số điểm cực trị của f(x) và số nghiệm đơn (hoặc bội lẻ) của phương trình f(x)=0
Chọn đáp án B.
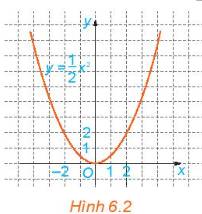
a) Dựa vào đồ thị của hàm số \(y=\dfrac{1}{2}x^2\)(H.6.2), tìm \(x\) sao cho \(y=8\).
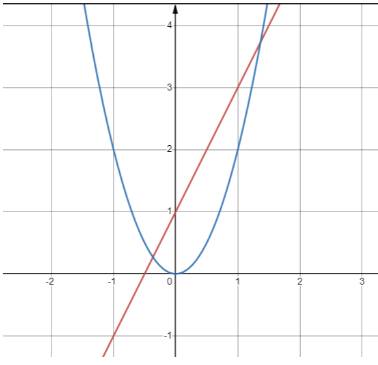
b) Vẽ đồ thị của các hàm số \(y=2x+1\) và \(y=2x^2\) trên cùng một mặt phẳng tọa độ.
a) Để \(y = 8 \Leftrightarrow \frac{1}{2}{x^2} = 8 \Leftrightarrow {x^2} = 16 \Leftrightarrow x = 4\) hoăc \(x = - 4\)
b) Vẽ đồ thị y=2x+1:
-Là đồ thị bậc nhất nên đồ thị là đường thẳng đi qua điểm có tọa độ (0; 1) và
(-1; -1)
Vẽ đồ thị \(y = 2{x^2}\)
- Đi qua điểm (1; 2) ; (-1; 2);(0;0)
Cho hàm số y=f(x). Hàm số y= f’(x) có đồ thị như hình vẽ dưới đây.
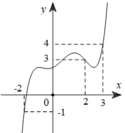
Đặt g ( x ) = 2 f ( x ) - x + 1 2 .Biết f(-2)=f(3). Mệnh đề nào đúng?
A. ![]()
B![]()
C. ![]()
D. ![]()
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y=(m+1)x-2 có đồ thị là đường thẳng d. Tìm m để đồ thị hàm số d cắt đồ thị hàm số y=x+3 tại điểm có tung độ là 2.