Tổng tất cả các số n thỏa mãn C n 1 + C n 2 ≥ C n 3 (trong đó C n k là tổ hợp chập k của n phần tử) là
A. 24
B. 23
C. 31
D. 18
Tìm tất cả các số tự nhiên n thỏa mãn bất phương trình: 2(n-1)-5(n-2>0.
`2(n-1)-5(n-2)>0`
`<=>2n-2-5n+10>0`
`<=>8-3n>0`
`<=>3n<8`
`<=>n<8/3`
Mà `n in NN`
`=>n in {0,1,2}`
\(2\left(n-1\right)-5\left(n-2\right)>0\)
<=> 2n -2 - 5n + 10 > 0
<=> -3n + 8 > 0
<=> -3n > - 8
<=> \(n< \dfrac{8}{3}\)
Mà n là số tự nhiên
<=> n \(\in\left\{0;1;2\right\}\)
\(2\left(n-1\right)-5\left(n-2\right)>0\)
\(\Leftrightarrow2n-2-5n+2>0\)
\(\Leftrightarrow2n-5n>0+2-2\)
\(\Leftrightarrow-3n>0\)
\(\Leftrightarrow\)\(n< 0\)
Vậy S={n|n<0}
biết số nguyên n thỏa mãn 13n chia hết cho n -1 tổng tất cả giá trị của n là
13n = 13n - 13 + 13
= 13(n - 1) + 13
Để 13n ⋮ (n - 1) thì 13 ⋮ (n - 1)
⇒ n - 1 ∈ Ư(13) = {-13; -1; 1; 13}
⇒ n ∈ {-12; 0; 2; 14}
Tổng của chúng là:
-12 + 0 + 2 + 14 = 4
ai trả lời nhanh bài nay dùm mình với mình đang
gấp
Tính tổng tất cả các số nghuyên x thỏa mãn|x-2|<-5
|x-2|>= 0 với mọi x
=>|x-2|< -5 là vô lí
Tổng tất cả các số tự nhiên n thỏa mãn 1 C n 1 - 1 C n + 1 2 = 7 6 C n + 4 1 là:
A. 11
B. 13
C. 12
D. 10
Tổng tất cả các số tự nhiên n thỏa mãn 1 C n 1 - 1 C n + 2 2 = 7 6 C n + 4 1 là:
A. 11
B. 13
C. 12
D. 10
Đáp án A
Phương pháp: 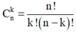
Cách giải: ĐK: n ≥ 1
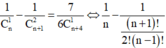
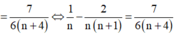
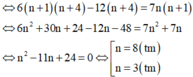
Tìm tất cả các số nguyên dương $n$ thỏa mãn:
$2^n+n|8^n+n$
Cái này không LATEX đc, đề là:
Tìm tất cả số nguyên dương n thỏa mãn:
\2^n+n|8^n+n\
Tổng tất cả các số n thỏa mãn C n 1 + C n 2 ≥ C n 3 (trong đó C n k là tổ hợp chập k của n phần tử) là
A. 24.
B. 23.
C. 31.
D. 18.
Tất cả các số tự nhiên n thỏa mãn (n + 13) chia hết (n-2)
Lời giải:
$n+13\vdots n-2$
$\Rightarrow (n-2)+15\vdots n-2$
$\Rightarrow 15\vdots n-2$
$\Rightarrow n-2\in\left\{\pm 1; \pm 3; \pm 5; \pm 15\right\}$
$\Rightarrow n\in \left\{3; 1; 5; -1; 7; -3; 17; -13\right\}$
Do $n$ là số tự nhiên nên $n\in\left\{3; 1; 5; 7; 17\right\}$
Tìm tất cả các số tự nhiên n thỏa mãn 3n+14⋮n+1
\(\Rightarrow3\left(n+1\right)+11⋮n+1\\ \Rightarrow11⋮n+1\\ \Rightarrow n+1\inƯ\left(11\right)=\left\{1;11\right\}\\ \Rightarrow n\in\left\{0;10\right\}\)