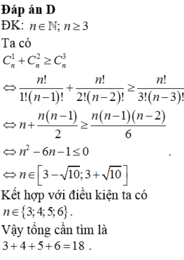Các câu hỏi tương tự
Với k và n là hai số nguyên dương tùy ý thỏa mãn k
≤
n. Công thức tính số tổ hợp chập k của n phần tử là
A
.
C
n
k
n
!
(
n
-
k
)
!
k
!
B
....
Đọc tiếp
Với k và n là hai số nguyên dương tùy ý thỏa mãn k ≤ n. Công thức tính số tổ hợp chập k của n phần tử là
A . C n k = n ! ( n - k ) ! k !
B . A n k = n ! ( n - k ) !
C . C n k = n ! ( n - k ) !
D . A n k = n ! ( n - k ) ! k !
Số các tổ hợp chập k của một tập hợp có n phần tử 1
≤
k
≤
n là :
A
.
C
n
k
n
!
(
n
-
k
)
!
B
.
C
n
k...
Đọc tiếp
Số các tổ hợp chập k của một tập hợp có n phần tử 1 ≤ k ≤ n là :
A . C n k = n ! ( n - k ) !
B . C n k = A n k k !
C . C n k = A n k ( n - k ) !
D . C n k = k ! ( n - k ) ! n !
Tìm số nguyên dương n thỏa mãn các điều kiện sau
C
n
-
1
4
-
C
n
-
1
3...
Đọc tiếp
Tìm số nguyên dương n thỏa mãn các điều kiện sau C n - 1 4 - C n - 1 3 < 5 4 A n - 2 2 C n + 1 n - 4 ≥ 7 15 A n + 1 3
(Ở đây A n k , C n k lần lượt là số chỉnh hợp và số tổ hợp chập k của n phần tử).
A. n=7
B. n=8
C. n=9
D. n=10
Với n là số nguyên dương thỏa mãn
A
n
k
+
2
A
n
2
100
(
A
n
k
là số các chỉnh hợp chập k của tập hợp có n phần tử). Số hạng chứa
x
5
trong khai triển của biểu thức...
Đọc tiếp
Với n là số nguyên dương thỏa mãn A n k + 2 A n 2 = 100 ( A n k là số các chỉnh hợp chập k của tập hợp có n phần tử). Số hạng chứa x 5 trong khai triển của biểu thức 1 + 3 x 2 n là:
A. 61236
B. 256 x 3
C. 252
D. 61236 x 3
Viết công thức tính số chỉnh hợp chập k của n phần tử, công thức tính số tổ hợp chập k của n phần tử. Cho ví dụ.
Kí hiệu
C
n
k
là số tổ hợp chập k của n phần tử (0
≤
k
≤
n). Mệnh đề nào sau đây đúng?
A
.
C
n
k
n
!
(
n
-
k
)
!...
Đọc tiếp
Kí hiệu C n k là số tổ hợp chập k của n phần tử (0 ≤ k ≤ n). Mệnh đề nào sau đây đúng?
A . C n k = n ! ( n - k ) !
B . C n k = n ! k !
C . C n k = n ! k ! ( n - k ) !
D . C n k = n ! k ! ( n - k ) !
Công thức tính số tổ hợp chập k của n phần tử là:
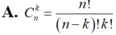
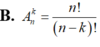
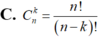
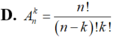
Phân biệt sự khác nhau giữa một chỉnh hợp chập k của n phần tử và một tổ hợp chập k của n phần tử.
Công thức tính số các chỉnh hợp chập k của một tập có n phần tử 1 ≤ k ≤ n là
A
.
C
n
k
n
!
(
n
-
k
)
!
B
.
C
n
k
...
Đọc tiếp
Công thức tính số các chỉnh hợp chập k của một tập có n phần tử 1 ≤ k ≤ n là
A . C n k = n ! ( n - k ) !
B . C n k = n ! k ! ( n - k ) !
C . A n k = n ! ( n - k ) !
D . A n k = n ! k ! ( n - k ) !