Tìm hệ số của x 5 trong khai triển biểu thức P = x 1 - 2 x n + x 2 1 + 3 x 2 n . Biết rằng A n 2 - C n + 1 n - 1 = 5
A. 3240
B. 3320
C. 3210
D. 3340
Tìm hệ số của x4 trong khai triển biểu thức (2x+1)(x-1)5
Hệ số của x^4 sẽ là tổng của 2*a và 1*b, với a là hệ số của x^3 trong (x-1)^5, b là hệ số của x^4 trong (x-1)^5
SHTQ là: \(C^k_5\cdot x^{5-k}\cdot\left(-1\right)^k=C^k_5\cdot\left(-1\right)^k\cdot x^{5-k}\)
Số hạng chứa x^3 tương ứng với 5-k=3
=>k=2
=>Hệ số là \(C^2_5\cdot\left(-1\right)^2=10\)
Số hạng chứa x^4 tương ứng với 5-k=4
=>k=1
=>Hệ số là \(C^1_5\cdot\left(-1\right)=-5\)
=>Hệ số của x^4 là: 2*10+1*(-5)=20-5=15
1/ Tìm hệ số x2 trong khai triển biểu thức :(3-2x)4
2/ Trong khai triển biểu thức (x-2y)4 hệ số của số hạng có xy3 là:
A.32
B.-24
C.-32
D.24
Ta có (x-2y)4 =[x+(-2y)]4=C4k.x4-k.(-2y)k
Hệ số của số hạng có xy3 ứng với : 4-k=1 va k=3 <=> k=3
Vậy hệ số của xy3 là : C43.(-2)3=-32
Tìm hệ số của x 5 trong khai triển biểu thức P = x ( 1 - 2 x ) n + x 2 ( 1 + 3 x ) 2 n . Biết rằng A n 2 - C n + 1 n - 1 = 5
A. 3240
B. 3320
C. 3210
D. 3340
Tìm hệ số của x 7 trong khai triển biểu thức sau: h ( x ) = x ( 2 + 3 x ) 9
A. 489889
B. 489887
C. -489888
D. 489888
Ta có ( 2 + 3 x ) 9 = ∑ k = 0 9 C 9 k 2 9 − k ( 3 x ) k = ∑ k = 0 9 C 9 k 2 9 − k 3 k . x k
⇒ h ( x ) = ∑ k = 0 9 C 9 k 2 9 − k 3 k x k + 1
Số hạng chứa x 7 ứng với giá trị k thỏa mãn k +1=7
Vậy hệ số chứa x 7 là: C 9 6 2 3 3 6 = 489888 .
Chọn đáp án D
Tìm hệ số của x 3 trong khai triển của biểu thức: x + 2 x 2 6
+ Số hạng tổng quát của khai triển 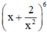 là:
là:
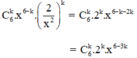
+ x3 ứng với 6 – 3k = 3 ⇔ k = 1.
Vậy hệ số của x3 là: 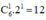
Tìm hệ số của \(x^2\) trong khai triển thành đa thức của biểu thức \(P=\left(x^2+x-1\right)^6\)
Theo công thức nhị thức Niu-tơn, ta có :
\(P=C_6^0\left(x-1\right)^6+C_6^1\left(x-1\right)^5+....+C_6^kx^{2k}\left(x-1\right)^{6-k}+....+C_6^5x^{10}\left(x-1\right)+C_6^6x^{12}\)
Suy ra, khi khai triển P thành đa thức, \(x^2\) chỉ xuất hiện khi khai triển \(C_6^0\left(x-1\right)^6\) và \(C_6^1\left(x-1\right)^5\)
Hệ số của \(x^2\) trong khai triển \(C_6^0\left(x-1\right)^6\) là : \(C_6^0.C_6^2\)
Hệ số của \(x^2\) trong khai triển \(C_6^1\left(x-1\right)^5\) là : \(-C_6^1.C_5^0\)
Vì vậy hệ số của \(x^2\) trong khai triển P thành đa thức là : \(C_6^0.C_6^2-C_6^1.C_5^0=9\)
Hệ số của x 5 trong khai triển biểu thức x ( 1 - 2 x ) 5 + x 2 ( 1 + 3 x ) 10 bằng.
A. 61268.
B. 61204.
C. 3160.
D. 3320.
Chọn D
Hệ số của
x
5
trong khai triển biểu thức
x
(
1
-
2
x
)
5
là hệ số của
x
4
trong khai triển biểu thức
(
1
-
2
x
)
5
và bằng ![]() .
.
Hệ số của
x
5
trong khai triển biểu thức
x
2
(
1
+
3
x
)
10
là hệ số của
x
3
trong khai triển biểu thức
(
1
+
3
x
)
10
và bằng ![]() .
.
Vậy hệ số của x 5 trong khai triển biểu thức x ( 1 - 2 x ) 5 + x 2 ( 1 + 3 x ) 10 bằng 3240 + 80 = 3320.
Tìm hệ số của x 4 trong khai triển P ( x ) = 1 - x - 3 x 3 n với n là số tự nhiên thỏa mãn hệ thức C n n - 2 + 6 n + 5 = A n + 1 2
A. 210
B. 840
C. 480
D. 270
Xác định hệ số của \({x^4}\) trong khai triển biểu thức \({\left( {3x + 2} \right)^5}\)
+) Ta có:
\(\begin{array}{l}{\left( {3x + 2} \right)^5} = {\left( {3x} \right)^5} + 5.{\left( {3x} \right)^4}2 + 10.{\left( {3x} \right)^3}{2^2} + 10{\left( {3x} \right)^2}{.2^3} + 5.\left( {3x} \right){.2^4} + {2^5}\\ = 243{x^5} + 810{x^4} + 1080{x^3} + 720{x^2} + 240x + 32\end{array}\)
+) Hệ số của \({x^4}\) trong khai triển trên là: \({a_4} = 810\)
Tìm hệ số của x 4 trong khai triển P ( x ) = ( 1 - x - 3 x 3 ) n với n là số tự nhiên thỏa mãn hệ thức C n n - 2 + 6 n + 5 = A n + 1 2
A. 210
B. 840
C. 480
D. 270