Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, đường cao S H = a 3 3 . Tính góc giữa cạnh bên và mặt đáy của hình chóp
![]()
![]()
![]()
![]()
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, đường cao S H = a 3 3 Tính góc giữa cạnh bên và mặt đáy của hình chóp
A. 45 o
B. 30 o
C. 75 o
D. 60 o
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi cạnh bên và mặt đáy.
\(+\) vì \(SH\perp\left(ABC\right)\) và \(AN\subset\left(ABC\right)\Rightarrow SH\perp AN\) hay \(\Rightarrow SH\perp AH\)
\(\Rightarrow\) \(AH\) là hình chiếu vuông góc của \(SA\) lên \(\left(ABC\right)\) \(\Rightarrow\left(SA,\left(ABC\right)\right)=\left(SA,AH\right)=\widehat{SAH}\)
\(+\) gọi \(M,N\) lần lượt là t/điểm \(AC,BC\)
vì \(\Delta ABC\) là tam giác đều cạnh \(a\) nên dễ tính được : \(AN=\dfrac{a\sqrt{3}}{2}\)
từ giả thiết , suy ra \(H\) là trọng tâm \(\Delta ABC\)
\(\Rightarrow\) \(AH=\dfrac{2}{3}AN=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
\(+\) áp dụng hệ thức lược trong tam giác \(SHA\) vuông tại \(H\) , có :
\(tan\widehat{SAH}\) \(=\dfrac{SH}{AH}=\dfrac{a}{\dfrac{a\sqrt{3}}{3}}=\sqrt{3}\Rightarrow\widehat{SAH}\) \(=60^o\)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên đáy là điểm H trên cạnh AC sao cho A H = 2 3 A C đường thẳng SC tạo với mặt phẳng đáy một góc 60 0 . Tính thể tích V của khối chóp S.ABC.
A. V = a 3 8
B. V = a 3 6
C. V = a 3 12
D. V = a 3 18
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên đáy là điểm H trên cạnh AC sao cho A H = 2 3 A C , đường thẳng SB tạo với mặt phẳng đáy một góc 45 0 . Tính thể tích V của khối chóp S.ABC.
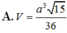
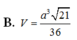
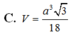
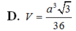
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên đáy là điểm H trên cạnh AC sao cho A H = 2 3 A C đường thẳng SC tạo với mặt phẳng đáy một góc 60 0 . Tính thể tích V của khối chóp S.ABC.
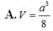
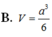
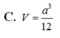

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên đáy là điểm H trên cạnh AC sao cho A H = 2 3 A C đường thẳng SB tạo với mặt phẳng đáy một góc 45 ° . Tính thể tích V của khối chóp S.ABC.
A. V = a 3 15 36
B. V = a 3 21 36
C. V = a 3 3 18
D. V = a 3 3 36
Bài 5. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên hợp với đáy một góc . Tính VS ABCD . theo a và . Bài 6. Tính thể tích khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc ASB = α . Áp dụng: Tính VS ABCD . trong trường hợp α = 60 độ.
Bài 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC =120độ . Cho SA vuông góc với đáy và SC = 2a .Tính thể tích hình chóp S.ABCD.
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là một hình thang cân (AB//CD) với AC=20 cm BC=15 cm AB=25 cm . Cho SA vuông góc với đáy và SA =18cm . Tính thể tích của khối chóp.
Bài 9. Cho hình chóp S.ABC có SA vuông góc với đáy. Mặt bên SBC là tam giác đều cạnh a. Cho gócBAC =120 . Tính VS ABC .
. Bài 10. Cho khối chóp S.ABC có đường cao SA bằng a, đáy là tam giác vuông cân có AB= BC= a . Gọi B' là trung điểm của SB, C' là chân đường cao hạ từ A của tam giác S.ABC:
a.Tính thể tích khối chóp S.ABC
b.Chứng minh SC vuông góc với (AB'C')
c.Tính thể tích khối chóp S.ABC
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và thể tích bằng 3a³. Tính chiều cao h của khối chóp S.ABC.
A. h = 12 3 a
B. h = 6 3 a
C. h = 4 3 a
D. h = 2 3 a
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA = 2HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60 o . Tính thể tích khối chóp S.ABCD.
A. a 3 3
B. a 42 12
C. a 42 8
D. a 3 12
Trong mặt phẳng (ABC), qua A kẻ đường thẳng d song song với BC. Kẻ H I ⊥ d , dễ thấy A I ⊥ S H I . Trong tam giác vuông SHI kẻ H K ⊥ S I , nhận thấy H K ⊥ S I A .
Ta có d S A , B C = d B , S I A = 3 2 d H , S I A = 3 2 H K
Ta tính được H = H A . sin 60 o = a 3 3
Ta có S C H ^ = S C ; A B C ^ , suy ra S H = a 21 3
Từ 1 H K 2 = 1 S H 2 + 1 H I 2 ta thu được H K = a 42 12
Suy ra d S A , B C = 3 2 H K = a 42 8
Đáp án C