2: Gọi A,B lần lượt là giao của (d) với trục Ox,Oy

Tọa độ A là:

y=0 và -5x+3=0

=>x=3/5 và y=0

Tọa độ B là:

x=0 và y=-5*0+3=3

=>A(3/5;0); B(0;3)

=>OA=0,6; OB=3

tan a=-5

=>a=101 độ

Ta có d: 4x + 2y = −5 ⇔ y = − 4 x − 5 2 và d’: 2x – y = −1 ⇔ y = 2x + 1

Xét phương trình hoành độ giao điểm của d và d’:

− 4 x − 5 2 = 2 x + 1 ⇔ −4x – 5 = 4x + 2 ⇔ 8x = −7 ⇔ x = − 7 8

⇒ y = 2 x + 1 = 2. − 7 8 + 1 = − 3 4

Vậy tọa độ giao điểm của d và d’ là − 7 8 ; − 3 4

Suy ra nghiệm của hệ phương trình 4 x + 2 y = − 5 2 x − y = − 1 là x 0 ;   y 0 = − 7 8 ; − 3 4

Từ đó x 0. y 0 = − 7 8 . − 3 4 = 21 32

Đáp án: A

a) Phương trình hoành độ giao điểm của (d₁) và (d₂):

-4x = x/2 + 3

⇔ x/2 + 4x = -3

⇔ 9x/2 = -3

⇔ x = -3 : 9/2

⇔ x = -2/3

⇒ y = -4.(-2/3) = 8/3

⇒ B(-2/3; 8/3)

b) Gọi (d): y = ax + b

Do (d) đi qua B(-2/3; 8/3) nên:

a.(-2/3)+ b = 8/3

⇔ b = 8/3 + 2a/3 (1)

Thay x = 1 vào (d₃) ta có:

y = 5.1 - 3 = 2

⇒ C(1; 2)

Do (d) cắt (d₃) tại C(1; 2) nên:

a.1 + b = 2

⇔ a + b = 2 (2)

Thay (1) vào (2) ta có:

a + 8/3 + 2a/3 = 2

⇔ 5a/3 = 2 - 8/3

⇔ 5a/3 = -2/3

⇔ a = -2/3 : 5/3

⇔ a = -2/5

Thay a = -2/5 vào (1) ta có:

b = 8/3 + 2/3 . (-2/5)

= 12/5

Vậy (d): y = -2x/5 + 12/5

Gọi I là giao điểm của ( d 1 ) và ( d 2 ). Khi đó tọa độ của I là nghiệm của hệ phương trình: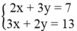 

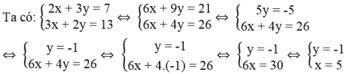
Tọa độ điểm I là I(5; -1)

Đường thẳng (d): y = (2m – 5)x – 5m đi qua I(5; -1) nên tọa độ của I nghiệm đúng phương trình đường thẳng:

Ta có: -1 = (2m – 5).5 – 5m ⇔ -1 = 10m – 25 – 5m

⇔ 5m = 24 ⇔ m = 24/5

Vậy với m = 24/5 thì đường thẳng (d) đi qua giao điểm của hai đường thẳng ( d 1 ) và ( d 2 ).

a: Thay m=2 vào y=(m-1)x+m-1, ta được:

y=(2-1)x+2-1=x+1

Phương trình hoành độ giao điểm là:

x+1=-x+1

=>2x=0

=>x=0

Thay x=0 vào y=x+1, ta được:

y=0+1=1

Vậy: Tọa độ giao điểm là A(0;1)

b: Thay x=3 và y=4 vào y=(m-1)x+m-1, ta được;

3(m-1)+m-1=4

=>4(m-1)=4

=>m-1=1

=>m=2

c: Để hai đường thẳng này cắt nhau thì \(m-1\ne-1\)

=>\(m\ne0\)

gọi giao điểm của 2 đường thẳng (d₁) và (d₂) là M(x₁,y₁)

Tọa độ giao điểm của đt (d₁) và (d₂) là nghiệm của hệ phương trình(hpt):

\(\left\{{}\begin{matrix}x_1-2y_1=1\\-3x_1+y_1=7\end{matrix}\right.< =>\left\{{}\begin{matrix}x_1=-3\\y_1=-2\end{matrix}\right.\) <=> M(-3;-2)

Vì đường thẳng mx-2y=n đi qua điểm A(2;1) và giao điểm của 2 đường thẳng trên nên ta có hpt:

\(\left\{{}\begin{matrix}2m-2=n\\-3m+4=n\end{matrix}\right.< =>^{ }\left\{{}\begin{matrix}m=\frac{6}{5}\\n=\frac{2}{5}\end{matrix}\right.\)

Vậy....

Tọa độ giao điểm của đường thẳng và đường tròn là nghiệm của hệ phương trình sau

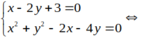
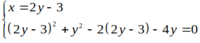
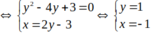hoặc 

Vậy tọa độ giao điểm là (3;3) và (-1; 1) .

Chọn A.

Bài 2 : 

\(\hept{\begin{cases}3x+2y=11\left(1\right)\\x+2y=5\left(2\right)\end{cases}}\)

Lấy phương trình (1) - phương trình (2) ta được : 

\(2x=6\Leftrightarrow x=3\)

Thay x = 3 vào phương trình (2) ta được : 

\(3+2y=5\Leftrightarrow2y=2\Leftrightarrow y=1\)

Vậy \(\left(x;y\right)=\left(3;1\right)\)

1 , a = 5 , b = -7

2 , x = 3 , y = 1