Tập hợp tất cả các giá trị thực của tham số m để hàm số y = - x 3 + 3 m - 1 x 2 + 3 4 m - 9 x - 1 đạt cực trị tại các điểm lớn hơn -1 là
A. 10 - 1 ; 4
B. - 1 - 10 ; 10 - 1
C. 10 - 1 ; + ∞
D. [ 10 - 1 ; + ∞ )
Những câu hỏi liên quan
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số
y
|
x
|
3
-
(
2
m
+
1
)
x
2
+
3
m
|
x
|
-
5
có 3 điểm cực trị. A.
-
∞
;
1...
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = | x | 3 - ( 2 m + 1 ) x 2 + 3 m | x | - 5 có 3 điểm cực trị.
A. - ∞ ; 1 4
B. 1 ; + ∞
C. ( - ∞ ; 0 ]
D. 0 ; 1 4 ∪ 1 ; + ∞
Cho hàm số
y
2
x
3
-
3
m
x
2
+
3
(
5
m
2
+
1
)
x
-
3
s
i
n
x
với m là tham số thực. Tìm tập hợp tất cả các giá trị của m để hàm số đồng biến trên (l;3).
A
.
m
≥
1...
Đọc tiếp
Cho hàm số y = 2 x 3 - 3 m x 2 + 3 ( 5 m 2 + 1 ) x - 3 s i n x với m là tham số thực. Tìm tập hợp tất cả các giá trị của m để hàm số đồng biến trên (l;3).
A . m ≥ 1
B . m ≤ - 1
C . m > 0
D . m ∈ R
14 tháng 5 2022 lúc 23:00
Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y=\left|x^3-3x^2+m-4\right|\) có đúng 5 điểm cực trị là?
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số
y
1
3
x
3
-
(
m
+
1
)
x
2
+
(
m
2...
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - ( m + 1 ) x 2 + ( m 2 + 2 m ) x - 3 nghịch biến trên khoảng ( 0 ; 1 )
A. [ - 1 ; + ∞ )
B. ( - ∞ ; 0 ]
C. [ - 1 ; 0 ]
D. [ 0 ; 1 ]
Tập hợp S tất cả các giá trị của tham số thực m để hàm số: y
1
3
x
3
-
(
m
+
1
)
x
2
+
(
m
2
+
2
m
)
x
-
3
nghịch biến trên khoảng (-1;1) là A. S
∅...
Đọc tiếp
Tập hợp S tất cả các giá trị của tham số thực m để hàm số: y = 1 3 x 3 - ( m + 1 ) x 2 + ( m 2 + 2 m ) x - 3 nghịch biến trên khoảng (-1;1) là
A. S = ∅
B. S = [0;1]
C. S = [-1;0]
D. S = {-1}
Chọn D.
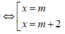
Do đó ta có bảng biến thiên sau:
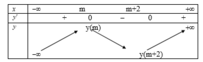
Để hàm số nghịch biến trên khoảng (-1;1) thì
Đúng 0
Bình luận (0)
Cho hàm số
y
1
3
x
3
+
2
x
2
+
(
m
+
2
)
x
-
m
. Tìm tập hợp S tất cả các giá trị thực của tham số m để hàm số đồng biến trên
ℝ
A.
S
(
-
∞
;
2
]
B.
S...
Đọc tiếp
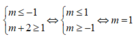
Cho hàm số y = 1 3 x 3 + 2 x 2 + ( m + 2 ) x - m . Tìm tập hợp S tất cả các giá trị thực của tham số m để hàm số đồng biến trên ℝ
A. S = ( - ∞ ; 2 ]
B. S = ( - ∞ ; 2 )
C. S = [ 2 ; + ∞ )
D. S = ( 2 ; + ∞ )
Tìm tập hợp S tất cả các giá trị của tham số thực m để hàm số
y
1
3
x
3
−
m
+
1
x
2
+
m
2
+
2
m
x
−
3
nghịch biến trên khoảng (-1;1). A. ...
Đọc tiếp
Tìm tập hợp S tất cả các giá trị của tham số thực m để hàm số y = 1 3 x 3 − m + 1 x 2 + m 2 + 2 m x − 3 nghịch biến trên khoảng (-1;1).
A. S = − 1 ; 0
B. S = ∅
C. S = − 1
D. S = 0 ; 1
Tìm tập hợp S tất cả các giá trị của tham số thực m để hàm số
y
1
3
x
3
-
m
+
1
x
2
+
m
2
+
2
m
x
-
3
nghịch biến trên khoảng
(...
Đọc tiếp
Tìm tập hợp S tất cả các giá trị của tham số thực m để hàm số y = 1 3 x 3 - m + 1 x 2 + m 2 + 2 m x - 3 nghịch biến trên khoảng ( - 1 ; 1 )
Tập hợp S tất cả các giá trị của tham số thực m để hàm số sau nghịch biến trên khoảng (-1;1):
y
1
3
x
3
-
m
+
1
x
2
+
m
2
+
2
m
x
-
3
A.
S
∅
B.
S...
Đọc tiếp
Tập hợp S tất cả các giá trị của tham số thực m để hàm số sau nghịch biến trên khoảng (-1;1): y = 1 3 x 3 - m + 1 x 2 + m 2 + 2 m x - 3
A. S = ∅
B. S = 0 ; 1
C. S = - 1 ; 0
D. S = - 1
cho hàm số y=\(\dfrac{x^2-m^2x+1}{x-1}\).Gọi S là tập hợp tất cả giá trị thực của tham số m để max=14/3