Cho cấp số cộng - 1 ; x ; 5 ; y . . Kết quả nào sau đây đúng?
A. x = 1 ; y = 7
B. x = 2 ; y = 7
C. x = 4 ; y = 8
D. x = 2 ; y = 8
Những câu hỏi liên quan
1) cho cấp số cộng left(u_nright) với u_12 và u_7-10 công sai của cấp số cộng là2) cho cấp số cộng left(u_nright) với u_11 và d 2 tổng S_{10}u_1+u_2+u_3...+u_{10} bằng3) cho cấp số cộng left(u_nright) có số hạng đầu u_13 và d 2. Tổng của 2019 số hạng đầu bằng4) cho cấp số cộng 2;5;8;11;14... công sai của cấp số cộng đã cho bằng5) cho cấp số cộng left(u_nright) với u_12 và d 9 khi đó số 2018 là số hạng thứ mấy trong dãy6) cho cấp số cộng left(u_nright) có số hạng đầu u_13 và d 2
Đọc tiếp
1) cho cấp số cộng \(\left(u_n\right)\) với \(u_1=2\) và \(u_7=-10\) công sai của cấp số cộng là
2) cho cấp số cộng \(\left(u_n\right)\) với \(u_1=1\) và d = 2 tổng \(S_{10}=u_1+u_2+u_3...+u_{10}\) bằng
3) cho cấp số cộng \(\left(u_n\right)\) có số hạng đầu \(u_1=3\) và d = 2. Tổng của 2019 số hạng đầu bằng
4) cho cấp số cộng 2;5;8;11;14... công sai của cấp số cộng đã cho bằng
5) cho cấp số cộng \(\left(u_n\right)\) với \(u_1=2\) và d = 9 khi đó số 2018 là số hạng thứ mấy trong dãy
6) cho cấp số cộng \(\left(u_n\right)\) có số hạng đầu \(u_1=3\) và d = 2
\(Bài.1:\\ u_7=u_1+6d\\ \Leftrightarrow-10=2+6d\\ \Rightarrow6d=-10-2=-12\\ Vậy:d=\dfrac{-12}{6}=-2\\ Bài.2:S_{10}=10.u_1+\dfrac{10.\left(10-1\right)}{2}.d=10.1+\dfrac{10.9}{2}.2=100\\ Bài.3:S_{2019}=2019.u_1+\dfrac{2019.\left(2019-1\right)}{2}.d\\ =2019.3+\dfrac{2019.2018}{2}.2=2019.2021=4080399\)
Đúng 1
Bình luận (0)
Bài 4:
\(d=u_2=u_1=5-2=3\)
Bài 5:
\(u_n=u_1+\left(n-1\right)d\\ \Leftrightarrow2018=2+\left(n-1\right).9\\ \Leftrightarrow2+9n-9=2018\\ \Leftrightarrow9n=2018-2+9\\ \Leftrightarrow9n=2025\\ \Leftrightarrow n=\dfrac{2025}{9}=225\)
Vậy: 2018 là số hạng thứ 225 của dãy
Bài 6:
Đề chưa có yêu cầu
Đúng 1
Bình luận (0)
4: d=u2-u1=3
5: Đặt 2018=2+(n-1)*9
=>9(n-1)=2016
=>n-1=224
=>n=225
=>2018 là số thứ 225
3:
\(S_{2019}=2019\left(\dfrac{2\cdot3+2018\cdot2}{2}\right)=4080399\)
2:
\(S_{10}=\dfrac{10\cdot\left(2\cdot1+9\cdot2\right)}{2}=10\left(1+9\right)=100\)
Đúng 0
Bình luận (0)
Cho cấp số cộng 1, 4, 7,... Số hạng thứ 100 của cấp số cộng là
A.297
B. 301.
C. 295.
D. 298.
Chọn D.
Cấp số cộng 1,4,7,.. có số hạng đầu u1 = 1 và công sai d = 3.
Đúng 0
Bình luận (0)
Cho cấp số cộng 1, 4, 7,... Số hạng thứ 100 của cấp số cộng là
A. 297
B. 301
C. 295
D. 298
Chọn D.
Cấp số cộng 1,4,7,.. có số hạng đầu u1 = 1 và công sai d = 3
Đúng 0
Bình luận (0)
Cho cấp số cộng \(u_1,u_2,u_3,...,u_n\) có công sai d, các số hạng của cấp số cộng đã cho đều khác 0. Với giá trị nào của d thì dãy số \(\dfrac{1}{u_1};\dfrac{1}{u_2};\dfrac{1}{u_3};...;\dfrac{1}{u_n}\) là một cấp số cộng?
Cho cấp số cộng \(u_1,u_2,u_3,...,u_n,...\) có công sai bằng 3. Biết dãy \(u_1,u_3,u_5,...,u_{2n+1}\) là cấp số cộng. Tính công sai của cấp số cộng đó?
Công sai của cấp số cộng đó là:
\(u_3-u_1=u_1+2d-u_1=2d=2\cdot3=6\)
Đúng 1
Bình luận (0)
Cho cấp số cộng (un) có u5=15;u9=-1. Tính u100 và S50 của cấp số cộng đó
Xem chi tiết
Hmm, cái công thức Sn mỗi lần viết dài kinh :(
\(u_5=u_1+4d=15;u_9=u_1+8d=-1\) \(\Rightarrow\left\{{}\begin{matrix}d=...\\u_1=...\end{matrix}\right.\)
\(\Rightarrow u_{100}=u_1+99d=...\)
\(u_1=u_1\)
\(u_2=u_1+d\)
\(u_3=u_1+2d\)
.....
\(u_n=u_1+\left(n-1\right)d\)
\(\Rightarrow S_n=u_1+u_2+...+u_n=u_1+u_1+d+...+u_1.\left(n-1\right)d=n.u_1+d+2d+...+\left(n-1\right)d\)
\(=n.u_1+\left(1+2+...+\left(n-1\right)\right)d=n.u_1+\dfrac{d\left(n-1\right).n}{2}=\dfrac{n\left[2u_1+\left(n-1\right)d\right]}{2}\)
Thay số vô và ... bấm máy, chắc zậy :))
Đúng 1
Bình luận (0)
1) trong các dãy số sau, dãy nào là một cấp số cộng
a) -8,-6,-4,-2,0,2
b) 1,4,7,10,12,15
c) 1,1,1,1,2,2,2
2) cho cấp số cộng \(u_n=3n+1\) tìm 4 số hạng đầu và công sai của cấp số cộng
1, Dãy a nha với d= 2
2,
\(u_1=3.1+1=4\\ u_2=3.2+1=7\\ d=u_2-u_1=7-4=3\)
Đúng 1
Bình luận (0)
Cho cấp số cộng (un) có số hạng đầu là u = 1 và công sai d = 1. Tìm n sao cho tổng n số hạng đầu tiên của cấp số cộng đó bằng 3003
Xem chi tiết
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Đúng 2
Bình luận (0)
Cho cấp số cộng (un) có số hạng đầu là u1 = 1 và công sai d = 1. Tìm n sao cho tổng của n số hạng đầu tiên của cấp số cộng đó bằng 3003.
A. n = 79
B. n = 78
C. n = 77
D. n = 80
Chọn C
- Do công sai và số hạng đầu là d = 1, u 1 = 1 nên đây là tổng của n số tự nhiên đầu tiên là:
Đúng 0
Bình luận (0)
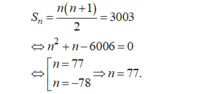
1) cho cấp số cộng \(\left(u_n\right)\) có \(u_1=-1\) và d =2. Tính \(u_6;u_{15};u_{80}\)
2) cho cấp số cộng \(\left(u_n\right)\) biết \(u_1=1\) và d = 4. Số 201 là số hạng thứ mấy
Xem lại đề câu 1
2,
\(u_{201}=u_1+\left(201-1\right).d=1+200.4=801\)
Đúng 0
Bình luận (0)