Tính tích phân sau I = ∫ 0 π 2 x cos x d x
A. I = π 2 + 1
B. I = 1 - π 2
C. I = π 2
D. I = π 2 - 1
Tính thể tích khối tròn xoay đó hình phẳng giới hạn bởi các đường sau quay quanh Ox:
y = cos x;y = 0; x = π
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường thẳng y = cos x , y = 0 , x = 0 , x = π quay quanh trục Ox.
A. π 3
B. π 2 2
C. π 2
D. π 2 3
\(\Leftrightarrow1-2sin^2x+\left(2m-3\right)sinx+m-2=0\)
\(\Leftrightarrow2sin^2x-\left(2m-3\right)sinx-m+1=0\)
\(\Leftrightarrow2sin^2x+sinx-2\left(m-1\right)sinx-\left(m-1\right)=0\)
\(\Leftrightarrow sinx\left(2sinx+1\right)-\left(m-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx+1\right)\left(sinx-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-\dfrac{1}{2}\\sinx=m-1\end{matrix}\right.\)
Pt có đúng 2 nghiệm thuộc khoảng đã cho khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1\ne-\dfrac{1}{2}\\-1\le m-1\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\0\le m\le2\end{matrix}\right.\)
Cho hai số thực a và b thỏa mãn a < b và ∫ a b x sin x d x = π đồng thời a cos a = 0 và b cos b = - π .Tính tích phân ∫ a b cos x d x .
A. I = - π .
B. I = π .
C. I = 145 12 .
D. I = 0.
Chọn D.
Đặt u = x d v = sin x d x ⇒ d u = d x v = - cos x
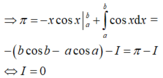
Dựa vào đồ thị y = cos x trên [-π,π] hãy chỉ ra các khoảng giá trị x mà cos x >0 , cos x < 0
Trong các khoảng sau, m thuộc khoảng nào để phương trình sin^2 x-(2m+1) sin x.cos x + 2m cos^2 x = 0 có nghiệm thuộc khoảng (π/4 ; π/3)?
\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)
Điện tích của một bản tụ điện trong một mạch dao động lí tưởng biến thiên theo thời gian theo hàm số q = q 0 cos ω t. Biểu thức của cường độdòng điện trong mạch sẽ là i = I 0 cos( ω t + φ ) với:
A. φ = 0. B. φ = π /2. C. φ = - π /2. D. φ = π .
Tính tích phân sau :
\(I=\int\frac{2dx}{2\sin x-\cos x+1}\)
Đặt \(t=\tan\frac{x}{2}\rightarrow dx=\frac{2dt}{1+t^2}\)
Khi đó : \(I=\int\frac{4\frac{dt}{1+t^2}}{\frac{4}{1+t^2}-\frac{1-t^2}{1+t^2}+1}=\int\frac{2dt}{1+2t^2}=\int\left(\frac{1}{t}-\frac{1}{t+2}\right)dt=\ln\left|\frac{1}{t+2}\right|+C=\ln\left|\frac{\tan\frac{x}{2}}{\tan\frac{x}{2}+2}\right|+C\)