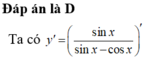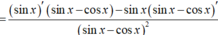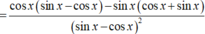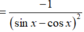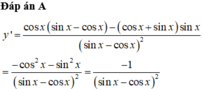Tìm đạo hàm của các hàm số sau y = sin 1 + x 2

Những câu hỏi liên quan
Tìm đạo hàm của mỗi hàm số sau:
a) \(y = \sin 3x + {\sin ^2}x\)
b) \(y = {\log _2}(2x + 1) + {3^{ - 2x + 1}}\)
a: \(y'=\left(sin3x\right)'+\left(sin^2x\right)'=3\cdot cos3x+sin\left(x+pi\right)\)
b: \(y'=\left(log_2\left(2x+1\right)\right)'+\left(3^{-2x+1}\right)'\)
\(=\dfrac{2}{\left(2n+1\right)\cdot ln2}-2\cdot3^{-2x+1}\cdot ln3\)
Đúng 1
Bình luận (0)
Tính đạo hàm của các hàm số sau:
a) \(y = x{\sin ^2}x;\)
b) \(y = {\cos ^2}x + \sin 2x;\)
c) \(y = \sin 3x - 3\sin x;\)
d) \(y = \tan x + \cot x.\)
tham khảo:
a)\(y'=xsin2x+sin^2x\)
\(y'=sin^2x+xsin2x\)
b)\(y'=-2sin2x+2cosx\\ y'=2\left(cosx-sin2x\right)\)
c)\(y=sin3x-3sinx\)
\(y'=3cos3x-3cosx\)
d)\(y'=\dfrac{1}{cos^2x}-\dfrac{1}{sin^2x}\)
\(y'=\dfrac{sin^2x-cos^2x}{sin^2x.cos^2x}\)
Đúng 1
Bình luận (0)
Tìm đạo hàm y' của hàm số y = sin x + cos x
A. y' = 2cosx
B. y' = 2sinx
C. y' = sinx - cosx
D. y' = cosx - sinx
Tính đạo hàm của các hàm số sau:
a) \(y = {e^{{x^2} - x}};\)
b) \(y = {3^{\sin x}}.\)
\(a,y'=\left(f\left(g\left(x\right)\right)\right)'\)
\(=f'\left(g\left(x\right)\right).g'\left(x\right)\)
\(=e^{g\left(x\right)}.\left(2x-1\right)\)
\(=e^{x^2-x}.\left(2x-1\right)\)
\(b,y'=\dfrac{d}{dx}\left(3^{sinx}\right)\)
\(=\dfrac{d}{dx}\left(e^{ln3.sinx}\right)\)
\(=\dfrac{d}{dx}\left(ln3.sinx\right).e^{ln3.sinx}\)
\(=ln3.cosx.3^{sinx}\)
Đúng 2
Bình luận (0)
Tính đạo hàm của các hàm số sau: (2 điểm)
a. $y={{\sin }^{3}}\left( {{x}^{2}}+2 \right)$;
b. $y={{\left( 2x+1 \right)}^{3}}{{\left( 3-{{x}^{2}} \right)}^{2}}$.
https://drive.google.com/file/d/14Q-YI3szy-rePnIHWGD35RKCWiCXCT6k/view?usp=sharing
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm đạo hàm của hàm số sau: y = sin ( cos 2 x ) . cos ( sin 2 x )
Tinh đạo hàm của các hàm số sau:
a) \(y = \tan \left( {{e^x} + 1} \right)\);
b) \(y = \sqrt {\sin 3x} \);
c) \(y = \cot \left( {1 - {2^x}} \right)\).
a: \(y'=\left[tan\left(e^x+1\right)\right]'=\dfrac{\left(e^x+1\right)'}{cos^2\left(e^x+1\right)}=\dfrac{e^x}{cos^2\left(e^x+1\right)}\)
b: \(y'=\left(\sqrt{sin3x}\right)'\)
\(=\dfrac{\left(sin3x\right)'}{2\sqrt{sin3x}}=\dfrac{3\cdot cos3x}{2\sqrt{sin3x}}\)
c: \(y=cot\left(1-2^x\right)\)
=>\(y'=\left[cot\left(1-2^x\right)\right]'\)
\(=\dfrac{-2}{sin^2\left(1-2^x\right)}\cdot\left(-2^x\cdot ln2\right)\)
\(=\dfrac{2^{x+1}\cdot ln2}{sin^2\left(1-2^x\right)}\)
Đúng 1
Bình luận (0)
Tính đạo hàm của hàm số sau
y
sin
x
sin
x
-
cos
x
Đọc tiếp
Tính đạo hàm của hàm số sau y = sin x sin x - cos x
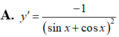
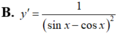
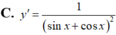

Tính đạo hàm của hàm số sau
y
sin
x
sin
x
-
cos
x
Đọc tiếp
Tính đạo hàm của hàm số sau y = sin x sin x - cos x
![]()
![]()
![]()
![]()
a) Gọi \(g\left( x \right)\) có đạo hàm của hàm số \(y = \sin \left( {2x + \frac{\pi }{4}} \right).\) Tìm \(g\left( x \right)\).
b) Tính đạo hàm của hàm số \(y = g\left( x \right)\).
a) \(g'\left( x \right) = y' = {\left( {2x + \frac{\pi }{4}} \right)^,}.\cos \left( {2x + \frac{\pi }{4}} \right) = 2\cos \left( {2x + \frac{\pi }{4}} \right)\)
b) \(g'\left( x \right) = - 2{\left( {2x + \frac{\pi }{4}} \right)^,}.\sin \left( {2x + \frac{\pi }{4}} \right) = - 4\sin \left( {2x + \frac{\pi }{4}} \right)\)
Đúng 0
Bình luận (0)