a: Xét (O) có

AB là tiếp tuyến

AC là tiếp tuyến

Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)

Ta có: OB=OC

nên O nằm trên đường trung trực của BC(2)

Từ (1) và (2) suy ra OA là đường trung trực của BC

=>OA⊥BC

Xét ΔOBA vuông tại B có BH là đường cao

nên \(OH\cdot OA=OB^2=R^2\)

b:Xét (O) có

ΔBCD nội tiếp

BD là đường kính

Do đó: ΔBCD vuông tại C

Suy ra: BC⊥CD

mà BC⊥AO

nên AO//CD

Ta có:
M_H = 1 amu
M_O = 16 amu
Ta có:
\(M_{H_2O}=1 . 2+16=18\left(amu\right)\) 
\(\%m_H=\dfrac{M_{H_2O}}{M_{H_2}} . 100\%=9\%\) 

\(\%m_O=100\%-9\%=91\%\) 
=> Nhận định trên là sai.

Trong phân tử nước gồm: 1 nguyên tử O và 2 nguyên tử H

Ta có: Khối lượng của nguyên tố O trong nước là:

m_O = 1 x 16 amu = 16 amu

Khối lượng của nguyên tố H trong nước là:

m_H = 2 x 1 amu = 2 amu

=> Khối lượng phân tử nước là: M_nước = 16 + 2 = 18 amu

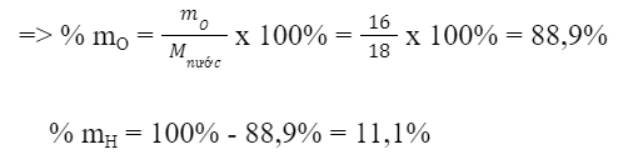
=> Ý kiến: Phần trăm khối lượng của H trong nước gấp 2 lần phần trăm khối lượng O là sai

                           Bài làm :

a) Ta có :

\(\widehat{ACB}\text{ là góc nội tếp chắn nửa đường tròn}\)

\(\Rightarrow\widehat{ACB}=90^o\Rightarrow\widehat{ACM}=180^o-\widehat{ACB}=90^o\)

Từ đó ; ta có :

\(\widehat{ACM}+\widehat{AHM}=90+90=180^o\)

=> Tứ giác AHMC là tứ giác nội tiếp đường tròn vì có 2 góc đối diện  = 180 độ 

=> Điều phải chứng minh

b) Theo phần a : Tứ giác AHMC là tứ giác nội tiếp 

\(\Rightarrow\widehat{AMH}=\widehat{ACH}\left(1\right)\)

Xét đường tròn (O) : Góc ADC và góc ABC đều là 2 góc nội tiếp cùng chắn cung AC

\(\Rightarrow\widehat{ADC}=\widehat{ABC}\left(2\right)\)

Vì CD⊥AB ; MH⊥AB

=> CD//MH 

=>∠ADC = ∠AMH ( 2góc so le trong ) (3)

Từ (1) ; (2) ; (3) 

\(\Rightarrow\widehat{ABC}=\widehat{ACH}\)

=> Điều phải chứng minh

c)∠AOC = 45^o

=>∠COB = 180 - 45 = 135^o

\(\Rightarrow S_{OCB}=\frac{\pi.R^2.n}{360}=\frac{\pi.2^2.135}{360}=\frac{3}{2}\pi\left(cm^2\right)\)

a) Xét tứ giác AHMC có 

góc ACM + góc AHM = 180 độ

Vậy tứ giác AHMC nội tiếp

Hình bạn tự vẽ nhé.

a) Xét \(\Delta ABH\) và \(\Delta ACH\) có:

AB=AC ( AB,AC là tiếp tuyến )

\(\widehat{BAH}=\widehat{CAH}\) ( AB,AC là tiếp tuyến )

AH là cạnh chung

\(\Rightarrow\Delta ABH=\Delta ACH\left(c-g-c\right)\)

\(\widehat{\Rightarrow BHA}=\widehat{CHA}\)( hai góc tương ứng )

Ta có : \(\widehat{BHA}+\widehat{CHA}=180^0\) ( hai góc kề bù )

mà \(\widehat{BHA}=\widehat{CHA}\left(cmt\right)\)

\(\Rightarrow\widehat{BHA}=\widehat{CHA}=90^0\)

\(\Rightarrow BC\perp AH\) hay \(BC\perp AO\)(đpcm)

b) Xét \(\Delta BAE\) và \(\Delta DAB\) có :

\(\widehat{BAD}\) là góc chung

\(\widehat{BDE}=\widehat{ABE}\) ( cùng chắn \(\stackrel\frown{BE}\))

\(\Rightarrow\Delta BAE\sim\Delta DAB\left(g-g\right)\)

\(\Rightarrow\frac{AE}{AB}=\frac{AB}{AD}\)

\(\Leftrightarrow AB^2=AE.AD\) (1)

Xét \(\Delta BAH\) và \(\Delta BOH\) cùng vuông góc tại H có:

\(AB^2=AH.AO\) ( hệ thức lượng trong tam giác vuông) (2)

Từ (1) và (2) \(\Rightarrow AE.AD=AH.AO\) (đpcm)

2) △OAB vuông tại B có BH là đường cao => AH.AO=BA²

tương tự △ABD vuông tại B có BE là đường cao => AE.AD = AB²

=> AH.AO=AE.AD

3) △OKA ∽ΔOHF => OK.OF=OH.OA=OB^2=OD^2
=> OK/OD=OD/OF
=>  Δ ODK ∽ ΔODF (c.g.c)
=>góc ODF = 90độ
=> FD là tt của (O)

Câu 1:

- Bộ não thỏ phát triển, đặc biệt là đại não, tiểu não liên quan đến hoạt động phong phú, phức tạp.
- Có cơ hoành tham gia vào hô hấp, phổi có nhiều túi phổi nhỏ làm tăng diện tích trao đổi khí.
- Tim 4 ngăn, hai vòng tuần hoàn, máu đi nuôi cơ thể đỏ tươi.
- Thận sau có cấu tạo phức tạp phù hợp với chức năng lọc máu.

Phản ứng với HCl chứng tỏ axit amino axetic có tính bazo (nhận proton H+)

Phản ứng với NaOH chứng tỏ axit amino axetic có tính axit (cho proton H+)

=> Axit amino axetic có tính lưỡng tính

=> Đáp án A

Hỏi nhiều vào! Mình đang thích học Hóa.Lâu rồi ko online Hóa