Hypebol 3x2- y2= 12 có tâm sai là:
A. e = 1 3
B. e = 1 2
C. e=2
D. e = 3
Bài 1: Thực hiện phép tính:
a) 2x.(3x2 – 5x + 3) b) (-2x-1).( x2 + 5x – 3 ) – (x-1)3
c) (2x – y).(4x2 + 2xy + y2) d) (6x5y2 – 9x4y3 + 15x3y4) : 3x3y2
e) (x3 – 3x2 + x – 3) : (x – 3)
Bài 2: Tìm x, biết:
a) 5x(x – 1) = 10 (x – 1); b) 2(x + 5) – x2 – 5x = 0;
c) x3 - x = 0; d) (2x – 1)2 – (4x – 3)2 = 0
e) (5x + 3)(x – 4) – (x – 5)x = (2x – 5)(5+2x )
Bài 3: Chứng minh rằng giá trị của biểu thức không phụ thuộc vào giá trị của biến.
a) x(3x + 12) – (7x – 20) + x2(2x – 3) – x(2x2 + 5).
b) 3(2x – 1) – 5(x – 3) + 6(3x – 4) – 19x.
Bài 4: Phân tích đa thức thành nhân tử.
a) 10x(x – y) – 8(y – x) b) (3x + 1)2 – (2x + 1)2
c) - 5x2 + 10xy – 5y2 + 20z2 d) 4x2 – 4x +4 – y2
e) 2x2 - 9xy – 5y2 f) x3 – 4x2 + 4 x – xy2
Bài 5: Tìm giá trị nhỏ nhất của biểu thức
a) A = 9x2 – 6x + 11 b) B = 4x2 – 20x + 101
Bài 6: Tìm giá trị lớn nhất của biểu thức
a) A = x – x2 b) B = – x2 + 6x – 11
a) 2x.(3x2 – 5x + 3)
=2x3-10x2+6x
b(-2x-1).( x2 + 5x – 3 ) – (x-1)3
=-2x3 - 10x2 + 6x - x2 - 5x + 3 - x3 + 3x2 - 3x + 1
= -3x3 - 8x2 - 2x + 4
d) (6x5y2 – 9x4y3 + 15x3y4) : 3x3y2
=2x2-3xy+5y2
Trong mặt phẳng Oxy, cho elip (E) có tâm sai e bằng 2 2 và cắt đường tròn (C) có phương trình x 2 + y 2 = 5 tại bốn điểm tạo thành hình chữ nhật ABCD có AB=2AD. Phương trình chính tắc của (E) là
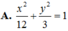
![]()
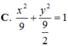
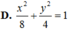
Cho mệnh đề:
1) Mặt cầu có tâm I 1 ; 0 ; - 1 , đường kính bằng 8 là: x - 1 2 + y 2 + z + 1 2 = 16
2) Mặt cầu có đường kính AB với A = - 1 ; 2 ; 1 , B = 0 ; 2 ; 3 là: x + 1 2 2 + y - 2 2 + z - 2 2 = 5 4
3) Mặt cầu có tâm O 0 ; 0 ; 0 và tiếp xúc với mặt cầu (S) có tâm 3 ; - 2 ; 4 , bán kính bằng 1 là: x 2 + y 2 + z 2 = 30 ± 2 29
Số mệnh đề đúng là bao nhiêu:
A. 1
B. 2
C. 3
D. 0
Khẳng định nào sau đây là sai?
(A) 3x2 y3 và 3x3 y2 là hai đơn thức đồng dạng;
(B) −3x2 y3và 3x2 y3 là hai đơn thức đồng dạng;
(C) (xy)2 và 3x2 y2 là hai đơn thức đồng dạng;
(D) -2(xy)3 và 5x3 y3 là hai đơn thức đồng dạng;
Đáp án đúng là (A) 3x2 y3 và 3x3 y2 là hai đơn thức đồng dạng.
Bài 1: Thực hiện phép tính:
a) x(3x2 – 2x + 5) b) 1/3 x2 y2 (6x + 2/3x2 – y)
c) ( 1/3x + 2)(3x – 6) d) ( 1/3x + 2)(3x – 6)
e) (x2 – 3x + 1)(2x – 5) f) ( 1/2x + 3)(2x2 – 4x + 6)
Bài 2: Tìm x, biết:
a) 3(2x – 3) + 2(2 – x) = –3 b) x(5 – 2x) + 2x(x – 1) = 13
c) 5x(x – 1) – (x + 2)(5x – 7) = 6 d) 3x(2x + 3) – (2x + 5)(3x – 2) = 8
Bài 3: Chứng tỏ rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến: a) A = x(2x + 1) – x2 (x + 2) + x3 – x + 3
b) B = (2x + 11)(3x – 5) – (2x + 3)(3x + 7) + 5
Bài 4: Tính giá trị của biểu thức
a) A = 2x( 1/2x2 + y) – x(x2 + y) + xy(x3 – 1) tại x = 10; y = – 1 10
b) B = 3x2 (x2 – 5) + x(–3x3 + 4x) + 6x2 tại x = –5
\(1,\\ a,=3x^3-2x^2+5x\\ b,=2x^3y^2+\dfrac{2}{9}x^4y^2-\dfrac{1}{3}x^2y^3\\ c,=x^2-2x+6x-12=x^2+4x-12\\ 2,\\ a,\Rightarrow6x-9+4-2x=-3\\ \Rightarrow4x=2\Rightarrow x=\dfrac{1}{2}\\ b,\Rightarrow5x-2x^2+2x^2-2x=13\\ \Rightarrow3x=13\Rightarrow x=\dfrac{13}{3}\\ c,\Rightarrow5x^2-5x-5x^2+7x-10x+14=6\\ \Rightarrow-8x=-8\Rightarrow x=1\\ d,\Rightarrow6x^2+9x-6x^2+4x-15x+10=8\\ \Rightarrow-2x=-2\Rightarrow x=1\)
\(3,\\ A=2x^2+x-x^3-2x^2+x^3-x+3=3\\ B=6x^2-10x+33x-55-6x^2-14x-9x-21=-76\)
Bài 4:
b: Ta có: \(B=3x^2\left(x^2-5\right)+x\left(-3x^3+4x\right)+6x^2\)
\(=3x^4-15x^2-3x^3+4x^2+6x^2\)
\(=-5x^2\)
\(=-5\cdot25=-125\)
Phân tích các đa thức sau thành nhân tử :
a) 3x2 – 7x + 2;
b) a(x2 + 1) – x(a2 + 1).;
c)(x+2)(x+3)(x+4)(x+5)-24;
d)(a+1)(a+3)(a+5)(a+7)+15;
e)x2 + 2xy + 7x + 7y + y2 + 10
(x2 là x bình,y 2 là y bình,a2 là a bình nha)
Giúp mình với:33
a) 3x2 – 7x + 2
\(=3x^2-6x-x+2\)
\(=\left(3x^2-6x\right)-\left(x-2\right)\)
\(=3x\left(x-2\right)-\left(x-2\right)\)
\(=\left(x-2\right)\left(3x-1\right)\)
b) a(x2 + 1) – x(a2 + 1)
\(=ax^2+a-\left(a^2x+x\right)\)
\(=a\left(x^2+1\right)-x\left(a^2+1\right)\)
.......?
a) Ta có: \(3x^2-7x+2\)
\(=3x^2-6x-x+2\)
\(=3x\left(x-2\right)-\left(x-2\right)\)
\(=\left(x-2\right)\left(3x-1\right)\)
b) Ta có: \(a\left(x^2+1\right)-x\left(a^2+1\right)\)
\(=x^2a+a-a^2x-x\)
\(=\left(x^2a-a^2x\right)+\left(a-x\right)\)
\(=xa\left(x-a\right)-\left(x-a\right)\)
\(=\left(x-a\right)\left(xa-1\right)\)
c) Ta có: \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
\(=\left(x^2+7x\right)^2+22\left(x^2+7x\right)+120-24\)
\(=\left(x^2+7x\right)^2+22\left(x^2+7x\right)+96\)
\(=\left(x^2+7x\right)^2+16\left(x^2+7x\right)+6\left(x^2+7x\right)+96\)
\(=\left(x^2+7x\right)\left(x^2+7x+16\right)+6\left(x^2+7x+16\right)\)
\(=\left(x^2+7x+16\right)\left(x^2+7x+6\right)\)
\(=\left(x^2+7x+16\right)\left(x+1\right)\left(x+6\right)\)
d) Ta có: \(\left(a+1\right)\left(a+3\right)\left(a+5\right)\left(a+7\right)+15\)
\(=\left(a^2+8a+7\right)\left(a^2+8a+15\right)+15\)
\(=\left(a^2+8a\right)^2+22\left(a^2+8a\right)+105+15\)
\(=\left(a^2+8a\right)^2+22\left(a^2+8a\right)+120\)
\(=\left(a^2+8a\right)^2+12\left(a^2+8a\right)+10\left(a^2+8a\right)+120\)
\(=\left(a^2+8a\right)\left(a^2+8a+12\right)+10\left(a^2+8a+12\right)\)
\(=\left(a^2+8a+12\right)\left(a^2+8a+10\right)\)
\(=\left(a+2\right)\left(a+6\right)\left(a^2+8a+10\right)\)
Phân tích đa thức thành nhân tử:
a.
b.
c.
d.
e.
g.
h.
a: 3x^2-12y^2
=3(x^2-4y^2)
=3(x-2y)(x+2y)
b: 5xy^2-10xyz+5xz^2
=5x(y^2-2yz+z^2)
=5x(y-z)^2
g: (a+b+c)^3-a^3-b^3-c^3
=(a+b+c-a)[(a+b+c)^2+a(a+b+c)+a^2]-(b+c)(b^2-bc+c^2)
=(b+c)[a^2+b^2+c^2+2ab+2ac+2bc+a^2+ab+ac+a^2-b^2+bc-c^2]
=(b+c)[3a^2+3ab+3bc+3ac]
=3(a+b)(b+c)(a+c)
1,phân tích mỗi đa thức sau thành phân tử
a,(x+2y)2-(x-y)2
b,(x+1)3+(x-1)3
c,9x2-3x+2y-4y2
d,4x2-4xy+2x-y+y2
e,x3+3x2+3x+1-y3
g,x3-2x2y+xy2-4x
a) \(\left(x+2y\right)^2-\left(x-y\right)^2=\left(x+2y+x-y\right)\left(x+2y-x+y\right)\)
\(=\left(2x+y\right).3y\)
b) \(\left(x+1\right)^3+\left(x-1\right)^3\)
\(=\left(x+1+x-1\right)\left[\left(x+1\right)^2-\left(x+1\right)\left(x-1\right)+\left(x-1\right)^2\right]\)
\(=2x\left[\left(x+1\right)^2-\left(x^2-1\right)+\left(x-1\right)^2\right]\)
c) \(9x^2-3x+2y-4y^2\)
\(=9x^2-4y^2-3x+2y\)
\(=\left(3x-2y\right)\left(3x+2y\right)-\left(3x-2y\right)\)
\(=\left(3x-2y\right)\left[3x+2y-1\right]\)
d) \(4x^2-4xy+2x-y+y^2\)
\(=4x^2-4xy+y^2+2x-y\)
\(=\left(2x-y\right)^2+2x-y\)
\(=\left(2x-y\right)\left(2x-y+1\right)\)
e) \(x^3+3x^2+3x+1-y^3\)
\(=\left(x+1\right)^3-y^3\)
\(=\left(x+1-y\right)\left[\left(x+1\right)^2+y\left(x+1\right)+y^2\right]\)
g) \(x^3-2x^2y+xy^2-4x\)
\(=x\left(x^2-2xy+y^2\right)-4x\)
\(=x\left(x-y\right)^2-4x\)
\(=x\left[\left(x-y\right)^2-4\right]\)
\(=x\left(x-y+2\right)\left(x-y-2\right)\)
a) (x + 2y)² - (x - y)²
= (x + 2y - x + y)(x + 2y + x - y)
= 3y(2x + y)
b) (x + 1)³ + (x - 1)³
= (x + 1 + x - 1)[(x + 1)² - (x + 1)(x - 1) + (x - 1)²]
= 2x(x² + 2x + 1 - x² + 1 + x² - 2x + 1)
= 2x(x² + 3)
c) 9x² - 3x + 2y - 4y²
= (9x² - 4y²) - (3x - 2y)
= (3x - 2y)(3x + 2y) - (3x - 2y)
= (3x - 2y)(3x + 2y - 1)
d) 4x² - 4xy + 2x - y + y²
= (4x² - 4xy + y²) + (2x - y)
= (2x - y)² + (2x - y)
= (2x - y)(2x - y + 1)
e) x³ + 3x² + 3x + 1 - y³
= (x³ + 3x² + 3x + 1) - y³
= (x + 1)³ - y³
= (x + 1 - y)[(x + 1)² + (x + 1)y + y²]
= (x - y + 1)(x² + 2x + 1 + xy + y + y²)
g) x³ - 2x²y + xy² - 4x
= x(x² - 2xy + y² - 4)
= x[(x² - 2xy + y²) - 4]
= x[(x - y)² - 2²]
= x(x - y - 2)(x - y + 2)
Cho E = {x ≤ Z||x| ≤ 5}, F = {x ∈ N ||x| ≤ 5} và
B = {x ∈ Z|(x – 2)(x + 1)(2x2 – x – 3) = 0}. Chứng minh A ⊂ E và B⊂E
Cho A = {x ∈ R | x2+ x – 12 = 0 và 2x2 – 7x + 3 = 0}
B = {x ∈ Z | 3x2 – 13x + 12 =0 hoặc x2 – 3x = 0}