Sử dụng tổng 3 góc tam giác

Những câu hỏi liên quan
Sử dụng Tổng 3 góc của tam giác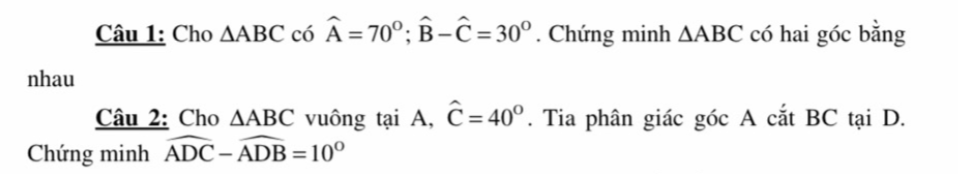
Câu 1:
\(\widehat{B}+\widehat{C}=110^0\)
\(\Leftrightarrow\widehat{B}=70^0;\widehat{C}=40^0\)
Vậy: ΔABC có hai góc bằng nhau
Đúng 0
Bình luận (1)
Trình bày( sử dụng tổng 3 góc tam giác) ạ
Câu 1:
\(\left\{{}\begin{matrix}b-c=30\\b+c=110\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=70\\c=40\end{matrix}\right.\)
Vậy: ΔABC có hai góc bằng nhau
Đúng 0
Bình luận (0)
Sử dụng tc góc trong, góc ngoài, tổng 3 góc tam giác ạ. Gợi ý cái nào lm trc cx đc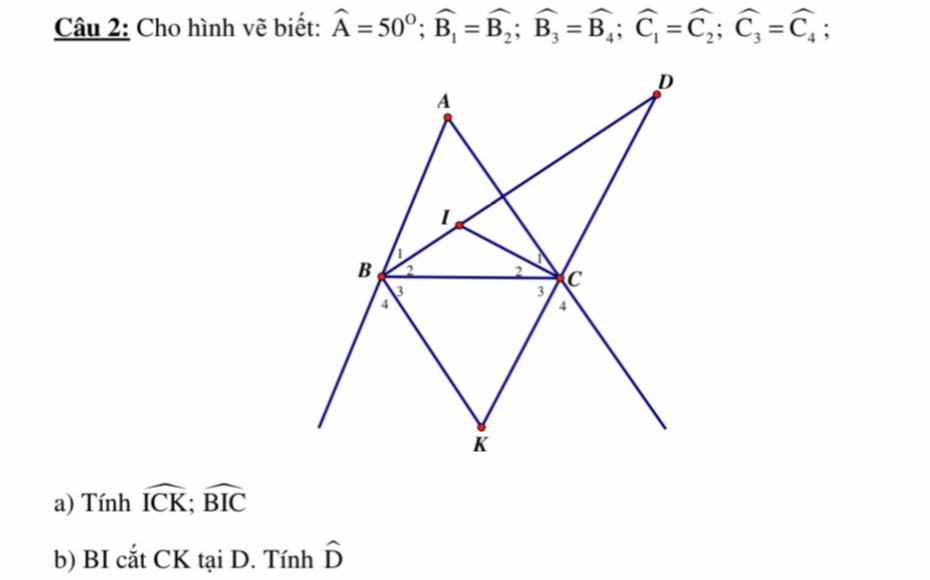
a. Gợi ý: \(\widehat{ICK}=\widehat{C_2}+\widehat{C_3}=\dfrac{1}{2}\left(\widehat{ACB}+\widehat{C}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
\(\widehat{BIC}=180^0-\left(\widehat{B_2}-\widehat{C_2}\right)=180^0-\dfrac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)=180^0-\dfrac{1}{2}\left(180^0-\widehat{BAC}\right)=180^0-90^0+\dfrac{1}{2}\widehat{BAC}=90^0+25^0=115^0\)
b. \(\widehat{ICK}=\widehat{D}+\widehat{CID}\Rightarrow\widehat{D}=90^0-\widehat{CID}=90^0-\left(180^0-\widehat{BIC}\right)=...\)
Đúng 0
Bình luận (0)
Sử dụng tổng 3 góc trong tam giác( gợi ý chi tiết cx đc ạ)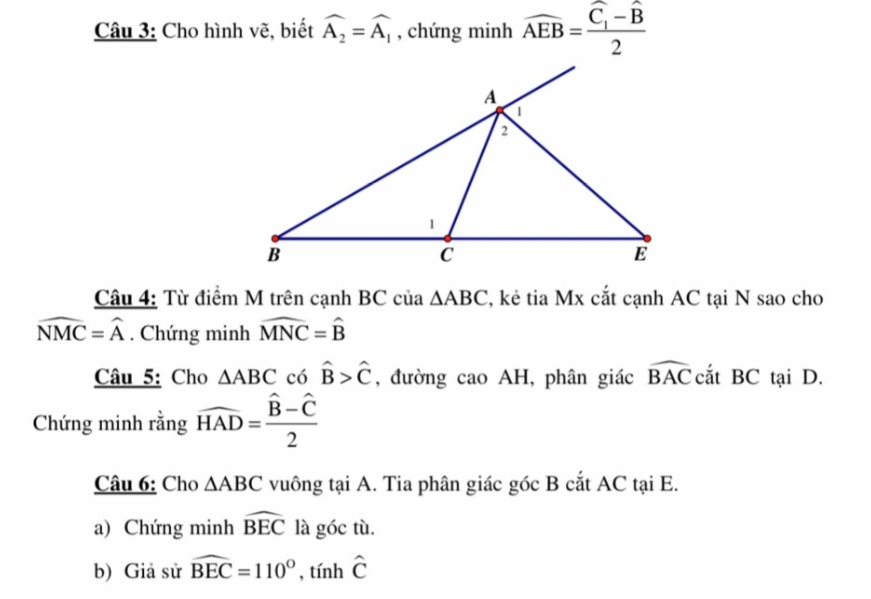
Sử dụng tổn 3 góc tam giác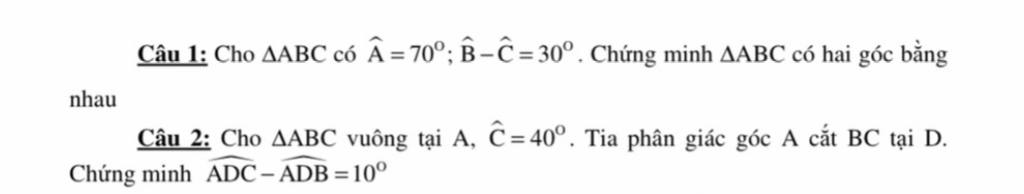
Câu 1:Xét ΔABC có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{B}+\widehat{C}=110^o\)
Rồi dùng tổng và hiệu tính được góc B và góc C rồi suy ra ĐPCM
Câu 2:
AD là phân giác góc A \(\Rightarrow\widehat{CAD}=\widehat{DAB}=\dfrac{\widehat{BAC}}{2}=45^o\)
Xét ΔACD có: \(\widehat{ADC}+\widehat{ACD}+\widehat{CAD}=180^o\Rightarrow\widehat{ADC}=95^o\)
Ta có: \(\widehat{ADC}+\widehat{ADB}=180^o\Rightarrow\widehat{ADB}=85^o\)
\(\widehat{ADC}-\widehat{ADB}=95^o-85^o=10^o\left(ĐPCM\right)\)
Đúng 2
Bình luận (1)
Cho tam giác đều ABC như hình 4.2.
1. Gọi tên các đỉnh, cạnh góc của tam giác đều ABC.
2. Dùng thước thẳng để đo và so sánh các cạnh của tam giác ABC.
3. Sử dụng thước đo góc để đo và so sánh các góc của tam giác ABC.
1) Các đỉnh : A, B, C
Các cạnh: AB, BC, AC
Các góc: \(\widehat A,\,\widehat B,\,\widehat C\)
2) AB =3 cm, AC = 3 cm, BC = 3 cm nên các cạnh của tam giác ABC bằng nhau
3) \(\widehat A = 60^0; \widehat B =60^0; \widehat C=60^0\) nên các góc của tam giác ABC bằng nhau và bằng 60o
Đúng 1
Bình luận (0)
Cho tam giác ABC và tam giác MNP có AB=MN, AC=MB, góc A = góc M. cmr : tam giác ABC=tam giác MNP ( ko sử dụng trường hợp cạnh góc cạnh nha )
1. Sử dụng hai góc kề bù có ba điểm nằm trên hai cạnh là hai tia đối nhau.
2. Ba điểm cùng thuộc một tia hoặc một một đường thẳng
3. Trong ba đoạn thẳng nối hai trong ba điểm có một đoạn thẳng bằng tổng hai đoạn thẳng kia.
4. Hai đoạn thẳng cùng đi qua hai trong ba điểm ấy cùng song song với đường thẳng thứ ba.
5. Hai đường thẳng cùng đi qua hai trong ba điểm ấy cùng vuông góc với đường thẳng thứ ba.
6. Đường thẳng cùng đi qua hai trong ba điểm ấy có chứa điểm thứ ba.
7. Sử dụng tính chất...
Đọc tiếp
\(1. Sử dụng hai góc kề bù có ba điểm nằm trên hai cạnh là hai tia đối nhau. 2. Ba điểm cùng thuộc một tia hoặc một một đường thẳng 3. Trong ba đoạn thẳng nối hai trong ba điểm có một đoạn thẳng bằng tổng hai đoạn thẳng kia. 4. Hai đoạn thẳng cùng đi qua hai trong ba điểm ấy cùng song song với đường thẳng thứ ba. 5. Hai đường thẳng cùng đi qua hai trong ba điểm ấy cùng vuông góc với đường thẳng thứ ba. 6. Đường thẳng cùng đi qua hai trong ba điểm ấy có chứa điểm thứ ba. 7. Sử dụng tính chất đường phân giác của một góc, tính chất đường trung trực của đoạn thẳng, tính chất ba đường cao trong tam giác . 8. Sử dụng tính chất hình bình hành. 9. Sử dụng tính chất góc nội tiếp đường tròn. 10. Sử dụng góc bằng nhau đối đỉnh 11. Sử dụng trung điểm các cạnh bên, các đường chéo của hình thang thẳng hàng 12. Chứng minh phản chứng 13. Sử dụng diện tích tam giác tạo bởi ba điểm bằng 0 14. Sử dụng sự đồng qui của các đường thẳng.\)













