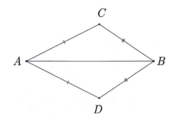
Cho hình vẽ bên. Chứng minh:
a) ∆ A B C = ∆ A B D
b) AB là phân giác của D A C ^
Những câu hỏi liên quan
Giúp mình với ạ
Cho Tam giác ABC vuông tại A(AB<AC) vẽ AK vuông góc với BC.Vẽ CM sao cho CA là tia phân giác của góc KCM.Qua A vẽ đường thẳng d sao cho d vuông góc với CM tại M.Từ B kẻ BH vuông góc với d
Chứng minh:a)CM=CK. b)AB là tia phân giác của HAK. c)So sánh AH và AM
Từ một điểm A bên ngoài (O), vẽ tiếp tuyến AB và cát tuyến ACD. Tia phân giác của góc B A C ^ cắt BC và BD lần lượt tại M và N. Vẽ dây BF vuông góc với MN, cắt MN tại H, cắt CD tại E. Chứng minh:
a, Tam giác BMN cân
b, F D 2 = F E . F B
cho tam giác ABC vuông tại A (AB<AC) tia phân giác của góc A cắt BC tại D qua D kẻ đường thẳng vuông góc với BC cắt AC tại E trên AB lấy điểm F sao cho AF=AE chứng minh:
a) Góc B= góc DEC
b) Tam giác DBE là tam giác cân
c)Chứng minh DB=DE
Cho hình thang ABCD, đấy lớn AD, góc BAD = góc CDA = 60o. Các cạnh AB = BC = CD = a. Chứng minh:
a, Đường phân giác trong của các góc B và góc C cắt nhau tại M là trung điểm của cạnh AD.
b, 4 điểm A, B, C, D nằm trên 1 đường tròn. Xác định tâm và bán kính của đường tròn.
a) Dễ dàng chứng minh góc BXC = 90
=> tam giác ABX đồng dạng với tam giác DXC => BX/CX = AB/DX => AB/BX = DX/CX (1)
=> tam giác ABX đồng dạng với tam giác XBC => AB/XB = AX/CX (2)
Từ (1), (2)
=> AX = DX => X là trung điểm AD
b) Từ câu a có tam giác ABX đồng dạng với tam giác DXC
=> AB.DC = AX.DX
Theo định lý pytago có:
BC^2 = BX^2 + CX^2 = AB^2 + AX^2 + DX^2 + CD^2 = (AB + CD)^2
=> BC = AB + CD
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A , vẽ tia Bx và Cy lần lượt vuông góc AB và AC sao cho Bx cắt Cy tại D (D và A nằm hai phía của đường thẳng BC). Chứng minh:
a)Tứ giác ABCD là hình chữ nhật.
b)Tứ giác ABCD có là hình vuông không ? vì sao ?
c)Chứng minh: AD vuông góc BC.
Cho tam giác ABC vuông cân tại A , vẽ tia Bx và Cy lần lượt vuông góc AB và AC sao cho Bx cắt Cy tại D (D và A nằm hai phía của đường thẳng BC). Chứng minh:
a)Tứ giác ABCD là hình chữ nhật.
b)Tứ giác ABCD có là hình vuông không ? vì sao ?
c)Chứng minh: AD vuông góc BC
cho điểm A bên ngoài (O) bán kính R từ A vẽ tiếp tuyến AB,AC và các tiếp tuyến A,D,E đến đường tròn tâm O.GỌI H là trung điiểm của DE(vẽ hình)
a)chứng minh 5 điểm: A,B,,H,O,C thẳng hàng
a) chứng minh:HA là tia phân giác của góc BHC
c) DE cắt BC tại I .CHỨNG MINH AB^2=AI.AH
Cho tam giác ABC có AB bằng AC . Kẻ tia phân giác của góc A cắt cạnh BC tại I. Chứng minh:
a) tam giác AIB = tam giác AIC ?
b) AI là đường trung trực của đoạn thẳng BC?
vẽ hình nữa nhé
a: Xét ΔABI và ΔACI có
AB=AC
\(\widehat{BAI}=\widehat{CAI}\)
AI chung
Do đó: ΔABI=ΔACI
Đúng 1
Bình luận (1)
Cho tam giác cân tại A( góc A<90 độ), vẽ BD vuông góc AC, CE vuông góc AB. Gọi H là giao điểm của BD và CE. Chứng minh:
a)AB//HK. b)Tam giác AKI cân.
c)AH là đường trung trực của ED. d)Trên tia đối của tia DB lấy điểm K sao cho DK=DB. Chứng minh góc ECB=DKC.
nhầm tiếp, phải là;
a) Tam giác ABD=ACE.
xin lỗi lần 2
Đúng 1
Bình luận (0)
a)Xét △ABD và △ACE:
góc ADB = góc AEC = 90o (BD vuông góc AC, CE vuông góc AB)
AB = AC (ΔABC cân tại A)
A là góc chung
Vậy △ABD = △ACE (ch.gn)
b) Ta có: △ABD = △ACE (cmt)
=>AD = AE (các cặp cạnh tương ứng)
=>△AED cân tại A
c) cho AF nằm trên AH sao cho AF\(\perp\)ED tại F
Xét △AFE và △AFD
góc AFE = góc AFD = 90o (AF\(\perp\)ED tại F)
AE = AD (cmt)
AF là cạnh chung
Vậy △AFE = △AFD (ch.cgv)
=>FE = FD (các cặp cạnh tương ứng)
=> F là trung điểm của ED
Vì AF nằm trên AH
=> AH đi qua trung điểm của AE và AH\(\perp\)ED
=>AH là đường trung trực của ED
d)Xét ΔECB và\(\Delta\)DBC
góc CEB = góc BDC = 90o ( BD vuông góc AC, CE vuông góc AB)
CB là cạnh chung
góc EBC = góc DCB (ΔABC cân tại A)
vậy ΔECB = \(\Delta\)DBC (ch.gn)
=> góc ECB = góc DBC (các cặp góc tương ứng)
Xét ΔCDB và ΔCDK
DB = DK (gt)
góc CDB = góc CDK = 90o (gt)
DC là cạnh chung
Vậy ΔCDB = ΔCDK (c.g.c)
=> góc CBD = góc CKD (các cặp góc tương ứng)
Mà góc CBD = góc ECB (cmt)
=> góc ECB=DKC
Đúng 1
Bình luận (1)