Số vị trí biểu diễn các nghiệm của phương trình tan 2 x - π 3 + 3 = 0 trên đường tròn lượng giác là?
A. 4
B. 3
C. 2
D. 1
Những câu hỏi liên quan
Số vị trí biểu diễn các nghiệm của phương trình tan 2 x − π 3 + 3 = 0 trên đường tròn lượng giác là?
A. 4
B. 3
C. 2
D. 1
Cho bất phương trình 2x ≤ 3.
a) Trong các số -2; 5/2; π; √10 số nào là nghiệm, số nào không là nghiệm của bất phương trình trên ?
b) Giải bất phương trình đó và biểu diễn tập nghiệm của nó trên trục số.
a) Ta có: 2. (-2) ≤ 3 nên -2 có là nghiệm của bất phương trình
+) 
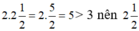không là nghiệm của bất phương trình ,
+) 2π > 3 nên π không là nghiệm của bất phương trình.
+) 
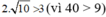nên √10 không là nghiệm của bất phương trình,
Các số là nghiệm của bất phương trình trên là: -2;
Các số không là nghiệm của bất phương trình trên là: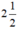 
; π; √10
b)2x ≤ 3 ⇔ x ≤ 3/2
Biểu diễn tập nghiệm trên trục số là:
Đúng 0
Bình luận (0)
Bài 1 tổng tất cả các nghiệm của phương trình sinx/cosx-1=0 trong đoạn [0;4π]
Bài 2 số vị trí biểu diễn tất cả các nghiệm của phương trình cos2x.tan x=0 trên đường tròn lượng giác là
Số vị trí điểm biểu diễn các nghiệm của phương trình
sin
2
x
+
2
cos
x
-
sin
x
-
1
tan
x
+
3
0
trên đường tròn luojng giác là bao nhiêu? A. 3 ...
Đọc tiếp
Số vị trí điểm biểu diễn các nghiệm của phương trình
sin 2 x + 2 cos x - sin x - 1 tan x + 3 = 0 trên đường tròn luojng giác là bao nhiêu?
A. 3
B. 1
C. 2
D. 4
Chọn D
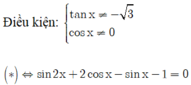
So với điều kiện, họ nghiệm của phương trình là
Đúng 0
Bình luận (0)
Số vị trí biểu diễn các nghiệm của phương trình : \(4cos^2x-4cosx-3=0\) trên đường tròn lượng giác là ?
A . 2
B . 0
C . 1
D . 4
Xem thêm câu trả lời
Số vị trí biểu diễn các nghiệm của phương trình tan3x=tanx trên đường tròn lượng giác là????
`tan3x=tanx`
`<=>3x=x+kπ`
`<=>x=k π/2`
Phương trình có `4` điểm biểu diễn các nghiệm: `π/2 ; π ; (3π)/2 ; 2π`.
Đúng 1
Bình luận (0)
Có 4 họ nghiệm được biểu diễn bởi các điểm A,B,C và D trên đường tròn đơn vị ở hình. Trong đó: Ứng với điểm A là họ nghiệm x 2k
π
Ứng với điểm B là họ nghiệm x
π
2
+
2
k
π
Ứng với điểm C là họ nghiệm x
π
+
2
k
π
Ứng với điểm D là họ nghiệm x
-
π
2
+
2
k...
Đọc tiếp
Có 4 họ nghiệm được biểu diễn bởi các điểm A,B,C và D trên đường tròn đơn vị ở hình. Trong đó:
Ứng với điểm A là họ nghiệm x = 2k π
Ứng với điểm B là họ nghiệm x = π 2 + 2 k π
Ứng với điểm C là họ nghiệm x = π + 2 k π
Ứng với điểm D là họ nghiệm x = - π 2 + 2 k π Phương trình cot3x=cotx có các họ nghiệm được biểu diễn bởi các điểm
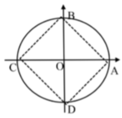
A. A và B
B. C và D
C. A và C
D. B và D
Đáp án D
Các họ nghiệm được biểu diễn bởi hai điểm A và C làm cho sin 3x = 0 và sin x = 0, do đó cot 3x và cot x không xác định
Đúng 0
Bình luận (0)
Bài 1: chọn ngẫu nhiên hai số khác nhau từ 30 số nguyên dương đầu tiên . Xác suất để chọn được hai số có tổng là một số chẵn bằng bao nhiêu?
bài 2: số vị trí biểu diễn các nghiệm của phương trình tan3x+cot(x-\(\dfrac{\pi}{2}\))=0 trên đường tròn lượng giác là?
1. Không gian mẫu: \(C_{30}^2\)
Trong 3 số nguyên dương đầu tiên có 15 số chẵn và 15 số lẻ
Hai số có tổng là chẵn khi chúng cùng chẵn hoặc lẻ
\(\Rightarrow C_{15}^2+C_{15}^2\) cách lấy 2 số có tổng chẵn
Xác suất: \(P=\dfrac{C_{15}^2+C_{15}^2}{C_{30}^2}=...\)
2. ĐKXĐ: \(x\ne\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow tan3x=cot\left(\dfrac{\pi}{2}-x\right)\)
\(\Leftrightarrow tan3x=tanx\)
\(\Rightarrow3x=x+k\pi\)
\(\Rightarrow x=\dfrac{k\pi}{2}\)
\(\Rightarrow x=k\pi\)
Có 2 điểm biểu diễn
Đúng 0
Bình luận (0)
Phương trình
tan (
x
+
π/
3)
có nghiệm là:
Đọc tiếp
Phương trình tan ( x + π/ 3) có nghiệm là:
