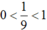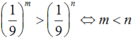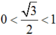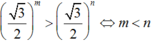Dùng dấu < , > , ≥ , ≤ để so sánh m và n nếu: m – n = 0

Những câu hỏi liên quan
Dùng dấu < , > , ≥ , ≤ để so sánh m và n nếu: m – n = 2
Ta có: m – n = 2 ⇒ m = n + 2 (1)
0 < 2 ⇒ 0 + n < 2 + n ⇒ n < n + 2 (2)
Từ (1) và (2) suy ra: n < m
Đúng 0
Bình luận (0)
Dùng dấu < , > , ≥ , ≤ để so sánh m và n nếu: n – m = 3
Ta có: n – m = 3 ⇒ n = m + 3 (3)
0 < 3 ⇒ 0 + m < 3 + m ⇒ m < m + 3 (4)
Từ (3) và (4) suy ra: m < n
Đúng 0
Bình luận (0)
Dùng dấu “<, >, ≥, ≤” để so sánh m và n nếu:
a. m – n = 2
b. m – n = 0
c. n – m = 3
a. nếu m-n=2 thì m>n
b. nếu m-n=0 thì m=n
c. nếu n-m=3 thì n>m hay m<n
theo mik nghĩ là thế!
nếu có j sai bảo mik vs nha!
Đúng 1
Bình luận (0)
a. Ta có:
m – n = 2 ⇒ m = n + 2 (1)
0 < 2 ⇒ 0 + n < 2 + n ⇒ n < n + 2 (2)
Đúng 3
Bình luận (0)
So sánh số hữu tỉ \(\frac{m}{n}\)(m,n thuộc Z, n khác 0) với 0 biết:
+/ m và n cùng dấu
+/ m và n khác dấu
Dùng "\(< ,>,\le,\ge\)" để so sánh \(m\) và \(n\) nếu :
a) \(m-n=2\)
b) \(m-n=0\)
c) \(n-m=3\)
1) So sánh số hữu tỉ a/b (a,b thuộc Z, b khác 0) vs số 0 khi a,b cùng dấu và khi a,b khác dấu.
2) Giả sử x=a/m, y=b/m (a,b,m thuộc Z, m>0) và x>y.Hãy chứng tỏ rằng nếu chọn z=a+b/2m thì ta có x<z<y. ( sử dụng tính chất: nếu a,b,m thuộc Z và a<b thì a+m<b+m)
1) Với a, b ∈ Z, b> 0
- Khi a , b cùng dấu thì \(\frac{a}{b}\) > 0
- Khi a,b khác dấu thì \(\frac{a}{b}\)< 0
Tổng quát: Số hữu tỉ \(\frac{a}{b}\) ( a,b ∈ Z, b # 0) dương nếu a,b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0
Đúng 0
Bình luận (0)
Theo đề bài ta có x = a/m, y = b/m (a, b, m ∈ Z, b # 0)
Vì x < y nên ta suy ra a < b
Ta có: x = 2a/2m, y = 2b/2m; z = (a+b)/2m
Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z < y
Đúng 0
Bình luận (0)
a) Hãy so sánh hai số tự nhiên sau đây, dùng kí hiệu "=" hay ">" để viết kết quả:
m = 12 036 001 và n = 12 035 987
b) Trên tia số (nằm ngang), trong hai điểm m và n, điểm nào nằm trước?
a) Vì hàng chục triệu, triệu, trăm nghìn, chục nghìn có các chữ số giống nhau, nhưng ở hàng nghìn ta thấy 6 > 5 nên 12 036 001 > 12 035 987. Vậy m>n
b) Vì m>n nên trên tia số điểm n nằm trước điểm m
Đúng 1
Bình luận (0)
So sánh hai số m và n nếu 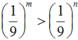
A. Không so sánh được.
B. m = n.
C. m > n.
D. m < n.
So sánh hai số m và n nếu 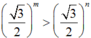
A. m < n
B. m = n
C. m > n
D. Không so sánh được