Cho tam giác ABC có a = 8 cm, b = 9 cm, c = 10 cm. Tam giác ABC là
A. Tam giác nhọn
B. Tam giác tù
C. Tam giác vuông
D. Tam giác đều
Những câu hỏi liên quan
Câu 1. Trong một tam giác vuông, kết luận nào sau đây là đúng ?A. Tổng hai góc nhọn bằng 180 0 B. Hai góc nhọn bằng nhauC. Hai góc nhọn phô nhau D. Hai góc nhọn kề nhau .Câu 2: Chọn câu trả lời đúng. Cho tam giác ABC có 00A50;B60 thì C?A. 70 0 B. 110 0 C. 90 0 D. 50 0Câu 3. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:A. 1cm ; 2cm ; 3cm B. 2cm ; 3cm ; 4cmC. 3cm ; 4cm ; 5cm D. 4cm ; 5cm ; 6cmCâu 4: Chọn câu sai.A. Tam giác có hai cạnh bằng nhau là tam giác cân...
Đọc tiếp
Câu 1. Trong một tam giác vuông, kết luận nào sau đây là đúng ?
A. Tổng hai góc nhọn bằng 180 0 B. Hai góc nhọn bằng nhau
C. Hai góc nhọn phô nhau D. Hai góc nhọn kề nhau .
Câu 2: Chọn câu trả lời đúng. Cho tam giác ABC có 00
A50;B60 thì C?
A. 70 0 B. 110 0 C. 90 0 D. 50 0
Câu 3. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
A. 1cm ; 2cm ; 3cm B. 2cm ; 3cm ; 4cm
C. 3cm ; 4cm ; 5cm D. 4cm ; 5cm ; 6cm
Câu 4: Chọn câu sai.
A. Tam giác có hai cạnh bằng nhau là tam giác cân.
B. Tam giác có ba cạnh bằng nhau là tam giác đều.
C. Tam giác cân là tam giác đều.
D. Tam giác đều là tam giác cân.
Câu 5: Tam giác ABC vuông tại B suy ra:
A. AB 2 = BC 2 + AC 2 B. BC 2 = AB 2 + AC 2
C. AC 2 = AB 2 + BC 2 D. Cả a,b,c đều đúng
Câu 6: Hãy điền dấu X vào ô trống mà em đã chọn :
Câu Nội dung Đúng Sai
1 Tam giác vuông có một góc bằng 045 là tam giác vuông cân
2 Tam giác cân có một góc bằng 060 là tam giác đều
3 Nếu ABC là một tam giác đều thì ABC là tam giác cân
4 Nếu hai cạnh và một góc của tam giác này bằng hai cạnh và
một góc của tam giác kia thì hai tam giác đó bằng nhau
Câu 7: a). Cho ABC vuông tại A có AB = 8 cm; AC = 6 cm thì BC bằng :
A. 25 cm B. 14 cm C. 100 cm D. 10 cm
b). Cho ABC cân tại A, biết 050B thì A bằng :
A. 080 B. 050 C. 0100 D. Đáp án khác
Câu 8 . Tam giác ABC có:
A. 0ABC90 B. 0ABC180 C. 0ABC45 D. 0ABC0
Câu 9: ABC = DEF Trường hợp cạnh – góc – cạnh nếu
A. AB = DE; BF ; BC = EF B. AB = EF; BF ; BC = DF
C. AB = DE; BE ; BC = EF D. AB = DF; BE ; BC = EF
Câu 10. Góc ngoài của tam giác bằng :
A. Tổng hai góc trong không kề với nó. B. Tổng hai góc trong
C. Góc kề với nó D. Tổng ba góc trong của tam giác.
Câu 1: C
Câu 2:A
Câu 3:C
Câu 4 C
Câu 5: B
Câu 6 1Đ, 2Đ, 3Đ, 4S
Câu 7: a, Đ
Câu 10 A.
Các câu khác k rõ đề
Cho tam giác ABC nhọn, có BE,AD là đường cao cắt ở H a) CM tam giác CDA đồng dạng tam giác CEB b) CM HA.HD=HB.HE c) CM tam giác ABC đồng dạng tam giác DEC d) Qua D kẻ đường thẳng vuông góc DE cắt BE tại M. CM góc ABC= góc EMD
a: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có
góc C chung
Do đó: ΔCDA\(\sim\)ΔCEB
b: Xét ΔHEA vuông tại E và ΔHDB vuông tại D có
\(\widehat{AHE}=\widehat{BHD}\)
Do đó: ΔHEA\(\sim\)ΔHDB
Suy ra: HE/HD=HA/HB
hay \(HE\cdot HB=HD\cdot HA\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có C=30°.Tia phân giác góc B cắt AC tại D.Trên cạnh BC lấy điểm M sao cho BM=BA
a) CM : tam giác ABD=tam giác MBD
b) CM: tam giác ABM là tam giác đều
c) CM : tam giác AMC là tam giác cân
d) Trên tia đối của tia AB lấy điểm E sao cho AB=AE. CM: AM//AC
cho tam giác ABC có AB=6cm, BC=10cm, AC=8cm
a, CM tam giác ABC vuông
b, Vẽ đường cao AH của tam giác ABC và phân giác AD của tam giác AHC. CM tam giác ABD là tam giác cân tại B
c, Vẽ phân giác AE của tam giác ABH. CM BD^2+CH^2=CE^2+BH^2
d, CM giao điểm của các đường trung trực của tam giác ADE cách đều 3 cạnh của tam giác ABC
Cho tam giác ABC. Vẽ điểm O cách đều ba đỉnh A, B, C trong mỗi trường hợp sau:
a) Tam giác ABC nhọn;
b) Tam giác ABC vuông tại A;
c) Tam giác ABC có góc A tù.
a) Tam giác ABC nhọn:
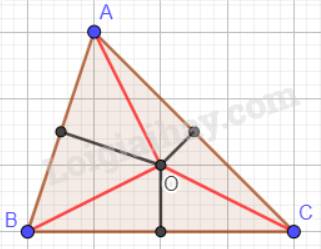
b) Tam giác ABC vuông tại A:
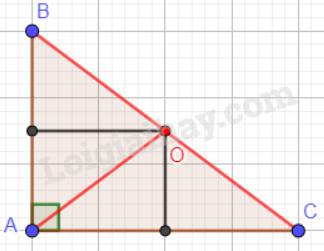
c) Tam giác ABC có góc A tù:
Đúng 0
Bình luận (0)
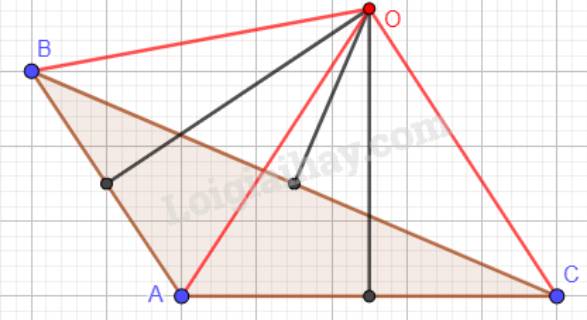
cần câu tl gấp: cho tam giác ABC vuông tại A, có B= 60 độ, AB= 5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E. a) CM: tam giác ABD= tam giác EBD. b) CM: tam giác ABE là tam giác đều. c) tính độ dài cạnh BC.
-Lưu ý: Chỉ mang tính chất tóm tắt bài làm, bạn không nên trình bày theo nhé!
a) △ABD và △EBD có: \(\widehat{ABD}=\widehat{EBD}\) (BD là tia phân giác của \(\widehat{ABC}\)) ; BD là cạnh chung ; \(\widehat{BAD}=\widehat{BED}=90^0\)
\(\Rightarrow\)△ABD=△EBD (c-g-c).
b) △ABD=△EBD (cmt) \(\Rightarrow AB=EB\) \(\Rightarrow\)△ABE cân tại B mà \(\widehat{ABC}=60^0\)
\(\Rightarrow\)△ABE đều.
c) \(\widehat{BAE}+\widehat{EAC}=90^0\Rightarrow60^0+\widehat{EAC}=90^0\Rightarrow\widehat{EAC}=30^0\)
\(\widehat{ABE}+\widehat{ACE}=90^0\Rightarrow60^0+\widehat{ACE}=90^0\Rightarrow\widehat{ACE}=30^0=\widehat{EAC}\)
\(\Rightarrow\)△AEC cân tại E. \(\Rightarrow AE=EC=AB=BE\)
\(\Rightarrow\)E là trung điểm BC và \(AB=\dfrac{1}{2}BC\)
\(\Rightarrow BC=10 \left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn , về phía ngoài tam giác vẽ các tam giác vuông cân tại A là tam giác ABD và ACE. Kẻ trung tuyến AM của tam giác ABC.
a) c/m: DE=2AM
b) c/m: AM vuông góc DE
c) CM: DC vuông góc BE
d) CM: DC=BE
cho tam giác ABC vuông tại A . Biết AB bằng 6 cm , BC = 10 cm a, tính AC và chu vi tam giác ABC b, kẻ BD là phân giác góc B . [ D thuộc AC ] . Từ D kẻ DM vuông góc với BC . CM tam giác ABD = tam giác MBD . c, So sánh AM và MC .
a. Áp dụng định lý pitago, ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC=\sqrt{10^2-6^2}=\sqrt{64}=8cm\)
\(C_{ABC}=6+8+10=24cm\)
b. xét tam giác vuông ABD và tam giác vuông BDM, có:
B : góc chung
AD: cạnh chung
Vậy tam giác vuông ABD = tam giác vuông BDM ( cạnh huyền - góc nhọn )
Đúng 3
Bình luận (0)
cho tam giác ABC có góc A=60°;góc B=3×góc C là tam giác:
A. tam giác vuông
B. tam giác nhọn
C. tam giác tù
D. tam giác cân
A. tam giác vuông
#Học tốt!!!
~NTTH~
\(\Delta ABC\)có \(\widehat{A}=60^o\)\(\Rightarrow\widehat{B}+\widehat{C}=120^o\)
mà \(\widehat{B}=3.\widehat{C}\)\(\Rightarrow4.\widehat{C}=120^o\)\(\Rightarrow\widehat{C}=30^o\)\(\Rightarrow\widehat{B}=90^o\)
\(\Rightarrow\Delta ABC\)vuông tại B