a) Tam giác ABC nhọn:
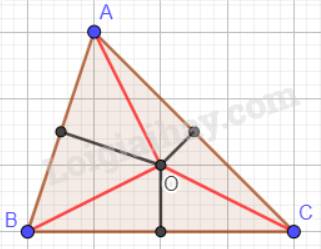
b) Tam giác ABC vuông tại A:
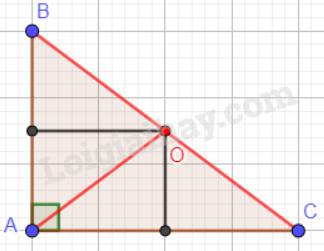
c) Tam giác ABC có góc A tù:
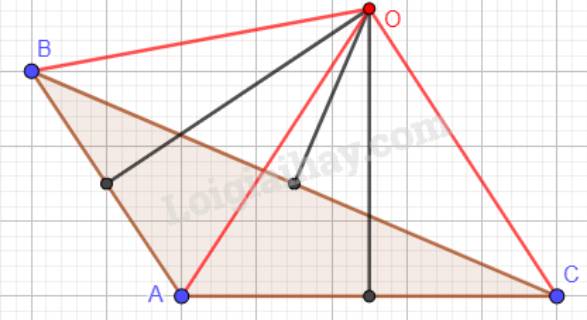
a) Tam giác ABC nhọn:

b) Tam giác ABC vuông tại A:

c) Tam giác ABC có góc A tù:

Tam giác ABC có ba đường trung tuyến cắt nhau tại G. Biết rằng điểm G cũng là giao điểm của ba đường trung trực trong tam giác ABC. Chứng minh tam giác ABC đều.
Tam giác ABC có ba đường phân giác cắt nhau tại I. Biết rằng I cũng là giao điểm ba đường trung trực của tam giác ABC. Chứng minh tam giác ABC đều.
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung trực của tam giác ABC.
Cho tam giác ABC và điểm O thỏa mãn OA = OB = OC. Chứng minh rằng O là giao điểm của ba đường trung trực của tam giác ABC.
Cho tam giác ABC. Đường trung trực của hai cạnh AB và AC cắt nhau tại điểm O nằm trong tam giác. M là trung điểm của BC. Chứng minh:
a) \(OM \bot BC\);
b) \(\widehat {MOB} = \widehat {MOC}\).
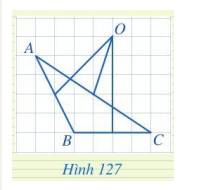
Trong Hình 127, điểm O có phải là giao điểm của ba đường trung trực của tam giác ABC không?
Quan sát các đường trung trực của tam giác ABC (Hình 126), cho biết ba đường trung trực đó có cùng đi qua một điểm hay không?
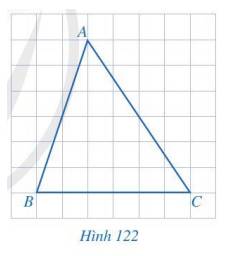
Cho tam giác ABC như Hình 122. Vẽ đường trung trực d của đoạn thẳng BC.
Hình 121 minh họa biển giới thiệu quần thể di tích, danh thắng cấp Quốc gia núi Dũng Quyết và khu vực Phượng Hoàng Trung Đô ở tỉnh Nghệ An (Hình 120).

Làm thế nào để xác định được vị trí cách đều ba địa điểm được minh họa trong Hình 121?