Hàm số y = sin x x có đạo hàm là
A. y ' = x cos x + sin x x 2
B. y ' = x cos x - sin x x 2
C. y ' = x sin x + c o s x x 2
D. y ' = x sin x - c o s x x 2
a) Gọi \(g\left( x \right)\) có đạo hàm của hàm số \(y = \sin \left( {2x + \frac{\pi }{4}} \right).\) Tìm \(g\left( x \right)\).
b) Tính đạo hàm của hàm số \(y = g\left( x \right)\).
a) \(g'\left( x \right) = y' = {\left( {2x + \frac{\pi }{4}} \right)^,}.\cos \left( {2x + \frac{\pi }{4}} \right) = 2\cos \left( {2x + \frac{\pi }{4}} \right)\)
b) \(g'\left( x \right) = - 2{\left( {2x + \frac{\pi }{4}} \right)^,}.\sin \left( {2x + \frac{\pi }{4}} \right) = - 4\sin \left( {2x + \frac{\pi }{4}} \right)\)
Cho hàm số \(u = \sin x\) và hàm số \(y = {u^2}\).
a) Tính \(y\) theo \(x\).
b) Tính \(y{'_x}\) (đạo hàm của \(y\) theo biến \(x\)), \(y{'_u}\) (đạo hàm của \(y\) theo biến \(u\)) và \(u{'_x}\) (đạo hàm của \(u\) theo biến \(x\)) rồi so sánh \(y{'_x}\) với \(y{'_u}.u{'_x}\).
a: \(y=u^2=\left(sinx\right)^2\)
b: \(y'\left(x\right)=\left(sin^2x\right)'=2\cdot sinx\cdot cosx\)
\(y'\left(u\right)=\left(u^2\right)'=2\cdot u\)
\(u'\left(x\right)=\left(sinx\right)'=cosx\)
=>\(y'\left(x\right)=y'\left(u\right)\cdot u'\left(x\right)\)
Tính đạo hàm của các hàm số sau:
a) \(y = x{\sin ^2}x;\)
b) \(y = {\cos ^2}x + \sin 2x;\)
c) \(y = \sin 3x - 3\sin x;\)
d) \(y = \tan x + \cot x.\)
tham khảo:
a)\(y'=xsin2x+sin^2x\)
\(y'=sin^2x+xsin2x\)
b)\(y'=-2sin2x+2cosx\\ y'=2\left(cosx-sin2x\right)\)
c)\(y=sin3x-3sinx\)
\(y'=3cos3x-3cosx\)
d)\(y'=\dfrac{1}{cos^2x}-\dfrac{1}{sin^2x}\)
\(y'=\dfrac{sin^2x-cos^2x}{sin^2x.cos^2x}\)
Tìm đạo hàm y' của hàm số y = sin x + cos x
A. y' = 2cosx
B. y' = 2sinx
C. y' = sinx - cosx
D. y' = cosx - sinx
Đạo hàm của hàm số y = sin x + log 3 x 3 (x > 0)
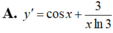
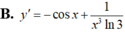
![]()
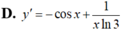
Tính đạo hàm của các hàm số sau:
a) \(y = {e^{{x^2} - x}};\)
b) \(y = {3^{\sin x}}.\)
\(a,y'=\left(f\left(g\left(x\right)\right)\right)'\)
\(=f'\left(g\left(x\right)\right).g'\left(x\right)\)
\(=e^{g\left(x\right)}.\left(2x-1\right)\)
\(=e^{x^2-x}.\left(2x-1\right)\)
\(b,y'=\dfrac{d}{dx}\left(3^{sinx}\right)\)
\(=\dfrac{d}{dx}\left(e^{ln3.sinx}\right)\)
\(=\dfrac{d}{dx}\left(ln3.sinx\right).e^{ln3.sinx}\)
\(=ln3.cosx.3^{sinx}\)
Tính đạo hàm của hàm số y = sin x - x cos x cos x + x sin x
A. ![]()
B. ![]()
C. 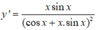
D. ![]()
Tính đạo hàm của hàm số sau y = sin x sin x - cos x
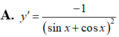
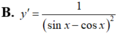
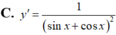

Tính đạo hàm của hàm số sau y = sin x sin x - cos x
![]()
![]()
![]()
![]()
Cho biết \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\). Dùng định nghĩa tính đạo hàm của hàm số \(y = \sin x\).
Với bất kì \({x_0} \in \mathbb{R}\), ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\sin x - \sin {x_0}}}{{x - {x_0}}}\)
Đặt \(x = {x_0} + \Delta x\). Ta có:
\(\begin{array}{l}f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin \left( {{x_0} + \Delta x} \right) - \sin {x_0}}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\cos \Delta x + \cos {x_0}\sin \Delta x - \sin {x_0}}}{{\Delta x}}\\ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\cos \Delta x - \sin {x_0}}}{{\Delta x}} + \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\cos {x_0}\sin \Delta x}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\left( {\cos \Delta x - 1} \right)}}{{\Delta x}} + \mathop {\lim }\limits_{\Delta x \to 0} \cos {x_0}.\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin \Delta x}}{{\Delta x}}\end{array}\)
Lại có:
\(\begin{array}{l}\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\left( {\cos \Delta x - 1} \right)}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\left( {\cos \Delta x - 1} \right)\left( {\cos \Delta x + 1} \right)}}{{\Delta x\left( {\cos \Delta x + 1} \right)}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\left( {{{\cos }^2}\Delta x - 1} \right)}}{{\Delta x\left( {\cos \Delta x + 1} \right)}}\\ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\left( { - {{\sin }^2}\Delta x} \right)}}{{\Delta x\left( {\cos \Delta x + 1} \right)}} = - \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin \Delta x}}{{\Delta x}}.\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}.\sin \Delta x}}{{\left( {\cos \Delta x + 1} \right)}} = - 1.\frac{{\sin {x_0}.\sin 0}}{{\cos 0 + 1}} = 0\\\mathop {\lim }\limits_{\Delta x \to 0} \cos {x_0}.\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin \Delta x}}{{\Delta x}} = \cos {x_0}.1 = \cos {x_0}\end{array}\)
Vậy \(f'\left( {{x_0}} \right) = \cos {x_0}\)
Vậy \(f'\left( x \right) = \cos x\) trên \(\mathbb{R}\).