Cho hình chóp S.ABCD có SC ⊥ (ABCD), đáy ABCD là hình thoi có cạnh bằng a 3 v à B C D ^ = 120 ° . Biết rằng góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 45°. Tính theo a thể tích khối chop S.ABCD.
A. 3 a 3 12
B. 3 3 a 3 2
C. 3 a 3 4
D. 3 3 a 3 4
cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, SA vuông góc với mặt phẳng đáy, SA=BD=a√3. Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) bằng
A. 60° B. 30° C.90° D.45°
Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.
Cho hình chóp S.ABCD có SC ⊥ (ABCD), đáy ABCD là hình thoi có cạnh bằng a 3 và ABC ^ = 120 o . Biết rằng góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 45°. Tính theo a thể tích khối chóp S.ABCD.
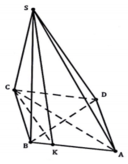
A. a 3 3 12
B. 3 a 3 3 12
C. a 3 3 4
D. 3 a 3 3 4
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa mặt bên hình chóp S.ABCD và mặt phẳng đáy có tang bằng:
A. 1
B. 3
C. 3 2
D. Đáp án khác
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa hai mặt bên hình chóp S.ABCD và mặt phẳng đáy có tan bằng:
A. 1
B. 3
C. 3 2
D. 2 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a, cạnh SAL(ABCD). Biết St= a/3, BAD = 1200. a) Chứng minh (SIC)L(SBD). b) Tính góc giữa SC với mặt phẳng (ABCD). c) Tính góc giữa hai mặt phẳng (SBC) và (ABCD). d) Tính khoảng cách giữa tôi và SC. c) "Gọi 7 là điểm bất kì thuộc đoạn thẳng $4. Dung thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng đi qua và vuông góc với St. Tìm vị trí điểm P để diện tích thiết diện thu được bằng một nửa diện tích hình thoi ABCD.
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: (SC;(ABCD))=(CS;CA)=góc SCA
Xét ΔBAC có BA=BC vàgóc BAC=60 độ
nên ΔBAC đều
=>AC=a
=>\(SC=\sqrt{SA^2+AC^2}=\dfrac{\sqrt{10}}{3}\cdot a\)
tan SCA=SA/AC=1/3
=>góc SCA=18 độ
Cho khối chóp S . A B C D có đáy A B C D là hình thoi cạnh a, S A = S B = S C = a , cạnh SD thay đổi. Thể tích lớn nhất của khối chóp S . A B C D bằng
A. a 3 8
B. a 3 2
C. 3 a 3 8
D. a 3 4
Đáp án là D.
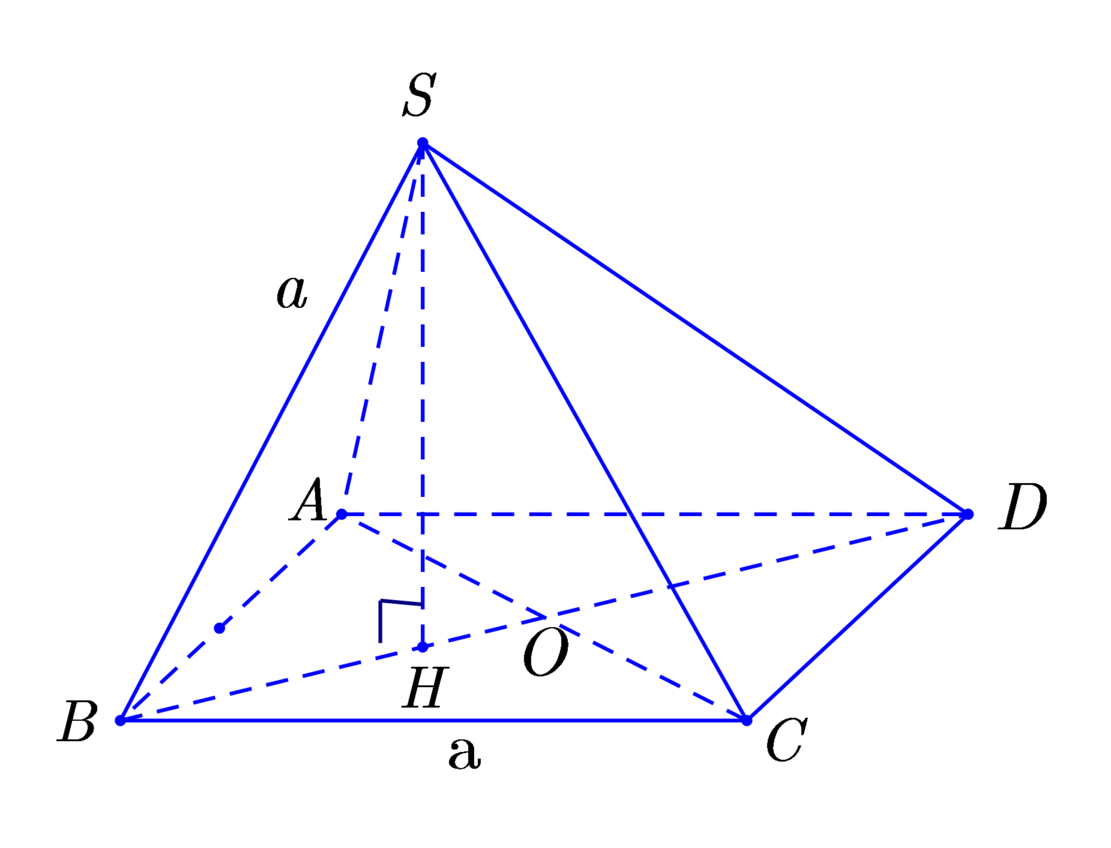
Khi SD thay đổi thi AC thay đổi. Đặt AC = x.
Gọi O = A C ∩ B D .
Vì S A = S B = S C nên chân đường cao SH trùng với tâm đường tròn ngoại tiếp tam giác ABC.
⇒ H ∈ B O
Ta có: O B = a 2 − x 2 2 = 4 a 2 − x 2 4 = 4 a 2 − x 2 2
S A B C = 1 2 O B . A C = 1 2 x . 4 a 2 − x 2 2 = x 4 a 2 − x 2 4
H B = R = a . a . x 4 S A B C = a 2 x 4. x 4 a 2 − x 2 4 = a 2 4 a 2 − x 2
S H = S B 2 − B H 2 = a 2 − a 4 4 a 2 − x 2 = a 3 a 2 − x 2 4 a 2 − x 2
S H = S B 2 − B H 2 = a 2 − a 4 4 a 2 − x 2 = a 3 a 2 − x 2 4 a 2 − x 2
= 1 3 a x . 3 a 2 − x 2 ≤ 1 3 a x 2 + 3 a 2 − x 2 2 = a 3 2
Cho hình chóp \(S.ABCD\) có đáy ABCD là hình thoi cạnh bằng 3cm. Các cạnh SA=SB=SC=3cm. Tam giác SBD có diện tích bằng 6cm3. Tính thể tích khối chóp \(S.ABCD\)
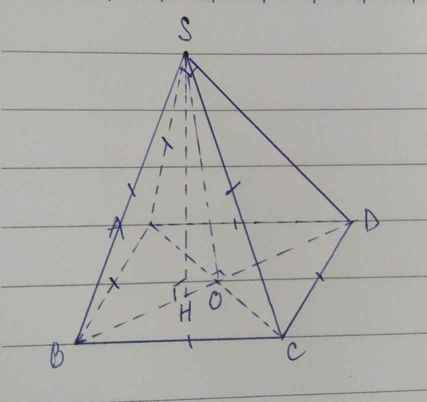
Gọi H là hình chiếu của S lên mp(ABCD), suy ra H thuộc BD (ABCD là hình thoi, SA=SB=SC).
Ta có: SA=SC=BA=BC=3 cm, suy ra SO=BO, suy ra tam giác SBD là tam giác vuông (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền).
0,5.SB.SD=6, suy ra SD=4 cm, suy ra BD=5 cm, AC=\(\sqrt{11}\) cm, SH=2,4 cm.
Thể tích cần tìm là V=1/3.2,4.0,5.5.\(\sqrt{11}\)=2\(\sqrt{11}\) (cm3).
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc A B C ^ = 60 ° . Biết SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng:
A. 60 °
B. 30 °
C. 45 °
D. 90 °
Chọn D.
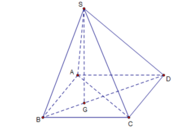
- Gọi G là trọng tâm tam giác ABC.
- Hình chóp S.ABC là hình chóp đều nên SG ⊥ (ABC).
→ Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 90 °
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Giả sử góc BAD bằng 60 o , khoảng cách từ S đến mặt phẳng (ABCD) bằng:
A. a 2
B. a 3 2
C. a
D. a 3