Cho hàm số f ( x ) = x 2 sin 1 x n ế u x ≠ 0 A n ế u x = 0
Xác định A để f(x) liên tục tại x = 0. Với giá trị A tìm được, hàm số có đạo hàm tại x = 0 không?
Những câu hỏi liên quan
SGK Cánh Diều
13 tháng 8 2023 lúc 22:34
Cho hàm số \(y = f(u) = \sin u;\,\,u = g(x) = {x^2}\)
a) Bằng cách thay u bởi \({x^2}\) trong biểu thức \(\sin u\), hãy biểu thị giá trị của y theo biến số x.
b) Xác định hàm số \(y = f(g(x))\)
a: \(y=f\left(x^2\right)=sin\left(x^2\right)\)
b: \(y=f\left(g\left(x\right)\right)=f\left(x^2\right)=sinx^2\)
Đúng 1
Bình luận (0)
Cho hàm số
f
(
x
)
sin
5
x
5
x
x
≠
0...
Đọc tiếp
Cho hàm số f ( x ) = sin 5 x 5 x x ≠ 0 a + 2 x = 0 . Tìm a để f(x) liên tục tại x = 0.
A. 1.
B. -1.
C. -2.
D. 2.
Chọn B.
Ta có: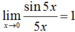 
; f(0) = a + 2.
Vậy để hàm số liên tục tại x = 0 thì a + 2 = 1 ⇔ a = -1.
Đúng 0
Bình luận (0)
14 tháng 4 2022 lúc 21:36
Cho hàm số fleft(xright)left{{}begin{matrix}2sin^2x+1,x 02^x;xge0end{matrix}right.. Giả sử Fleft(xright) là một nguyên hàm của hàm số fleft(xright) trên R và thỏa mãn điều kiện Fleft(1right)dfrac{2}{ln2}. Tính Fleft(-piright) A. Fleft(-piright)-2pi+dfrac{1}{ln2} B. Fleft(-piright)-2pi-dfrac{1}{ln2}C. Fleft(-piright)-pi-dfrac{1}{ln2} D. Fleft(-piright)-2piMình cần bài giải ạ, mình cảm ơn nhiều ♥
Đọc tiếp
Cho hàm số \(f\left(x\right)=\left\{{}\begin{matrix}2\sin^2x+1,x< 0\\2^x;x\ge0\end{matrix}\right.\). Giả sử \(F\left(x\right)\) là một nguyên hàm của hàm số \(f\left(x\right)\) trên \(R\) và thỏa mãn điều kiện \(F\left(1\right)=\dfrac{2}{ln2}\). Tính \(F\left(-\pi\right)\)
A. \(F\left(-\pi\right)=-2\pi+\dfrac{1}{ln2}\) B. \(F\left(-\pi\right)=-2\pi-\dfrac{1}{ln2}\)
C. \(F\left(-\pi\right)=-\pi-\dfrac{1}{ln2}\) D. \(F\left(-\pi\right)=-2\pi\)
Mình cần bài giải ạ, mình cảm ơn nhiều ♥
Xem thêm câu trả lời
Tìm nguyên hàm của hàm số
f
(
x
)
(
sin
x
+
c
o
s
x
)
2
A.
∫
f
(
x
)
d
x
x
+
1
2
c
o
s...
Đọc tiếp
Tìm nguyên hàm của hàm số f ( x ) = ( sin x + c o s x ) 2
A. ∫ f ( x ) d x = x + 1 2 c o s 2 x + C
B. ∫ f ( x ) d x = 1 2 c o s 2 x + C
C. ∫ f ( x ) d x = - 1 2 c o s 2 x + C
D. ∫ f ( x ) d x = x - 1 2 c o s 2 x + C
Nguyên hàm của hàm số
f
(
x
)
sin
x
.
2
−
cos
x
là A.
F
(
x
)
2
3
(
2
−
cos
x
)
2
−
cos
x
+
C
B.
F
(
x...
Đọc tiếp
Nguyên hàm của hàm số f ( x ) = sin x . 2 − cos x là
A. F ( x ) = 2 3 ( 2 − cos x ) 2 − cos x + C
B. F ( x ) = − 3 2 ( 2 − cos x ) 2 − cos x + C
C. F ( x ) = − 1 2 2 − cos x + C
D. F ( x ) = 2 3 2 − cos x + C
Cho hàm số yf(x). Hàm số f(x) có biến thiên Bất phương trình f(sin x) -3x + m đúng với mọi
x
∈
-
π
2
;
π
2
khi và chỉ khi A.
m
≥
f
(
1
)
+
3
π...
Đọc tiếp
Cho hàm số y=f(x). Hàm số f'(x) có biến thiên
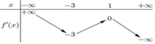
Bất phương trình f(sin x)< -3x + m đúng với mọi x ∈ - π 2 ; π 2 khi và chỉ khi
A. m ≥ f ( 1 ) + 3 π 2
B. m > f ( - 1 ) - 3 π 2
C. m > f ( π 2 ) + 3 π 2
D. m > f ( 1 ) + 3 π 2
cho hàm số f(x)=\(\left(sin^23x-4\right)^5\) có đạo hàm là \(f'\left(x\right)=k\left(sin^23x-4\right)^4.sin3xcos3x\). hỏi k bằng bao nhiêu
Lời giải:
$f'(x)=5(\sin ^23x-4)'(\sin ^23x-4)^4=5.2.\sin 3x (\sin 3x)'.(\sin ^23x-4)^4$
$=30\sin 3x\cos 3x(\sin ^23x-4)^4$
$\Rightarrow k=30$
Đúng 2
Bình luận (0)
Tìm họ nguyên hàm của hàm số :
\(f\left(x\right)=\frac{5\sin x}{2\sin x-\cos x+1}\)
Biến đổi :
\(5\sin x=a\left(2\sin x-\cos x+1\right)+b\left(2\cos x+\sin x\right)+c\)
= \(\left(2a+b\right)\sin x+\left(2b-a\right)\cos x+a+c\)
Đồng nhất hệ số hai tử số :
\(\begin{cases}2a+b=5\\2b-a=0\\a+c=0\end{cases}\)
\(\Rightarrow\) \(\begin{cases}a=2\\b=1\\c=-2\end{cases}\)
Khi đó :
\(f\left(x\right)=\frac{2\left(2\sin x-\cos x+1\right)+\left(2\cos x+\sin x\right)-2}{2\sin x-\cos x+1}\)
= \(2+\frac{2\cos x+\sin x}{2\sin x-\cos x+1}-\frac{2}{2\sin x-\cos x+1}\)
Do vậy :
\(I=2\int dx+\int\frac{\left(2\cos x+\sin x\right)dx}{2\sin x-\cos x+1}-2\int\frac{dx}{2\sin x-\cos x+1}\)
=\(2x+\ln\left|2\sin x-\cos x+1\right|-2J+C\)
Với
\(J=\int\frac{dx}{2\sin x-\cos x+1}\)
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
17 tháng 8 2023 lúc 16:44
Cho hàm số \(f(x) = {x^2} + {\sin ^3}x\). Khi đó \(f'\left( {\frac{\pi }{2}} \right)\) bằng
A. \(\pi \).
B. \(2\pi \).
C. \(\pi + 3\).
D. \(\pi - 3\).
\(f'\left(x\right)=2x+3sin^2\left(x\right)cos\left(x\right)\\ \Rightarrow f'\left(\dfrac{\pi}{2}\right)=\pi\)
\(\Rightarrow\) Chọn A.
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
17 tháng 8 2023 lúc 16:42
Cho hàm số \(f\left( x \right) = 2{\sin ^2}\left( {x + \frac{\pi }{4}} \right).\) Chứng minh rằng \(\left| {f''\left( x \right)} \right| \le 4\) với mọi x.
Ta có \(f'\left( x \right) = 2.2\sin \left( {x + \frac{\pi }{4}} \right).{\left[ {\sin \left( {x + \frac{\pi }{4}} \right)} \right]^,} = 4\sin \left( {x + \frac{\pi }{4}} \right)\cos \left( {x + \frac{\pi }{4}} \right) = 2\sin \left( {2x + \frac{\pi }{2}} \right)\)
\( \Rightarrow f''\left( x \right) = 2.2\cos \left( {2x + \frac{\pi }{2}} \right) = 4\cos \left( {2x + \frac{\pi }{2}} \right)\)
Mặt khác \( - 1 \le \cos \left( {2x + \frac{\pi }{2}} \right) \le 1 \Leftrightarrow - 4 \le f''\left( x \right) \le 4\)
Vậy \(\left| {f''\left( x \right)} \right| \le 4\) với mọi x.
Đúng 0
Bình luận (0)